
Validation of liquid chromatography mass spectrometry (LC-MS) methods
9.3. Estimation of LoD
Different approaches to estimate
http://www.uttv.ee/naita?id=23291
https://www.youtube.com/watch?v=xk2Ou3jaovg
There are a multitude of different approaches that can be used to estimate LoD, and no clear consensus exists on which approach is the best in different situations. The approach that we recommend in this course is discussed below in the video “Important aspects of estimating LoD and , ” and in the tutorial review [ and ]. A general overview of approaches from most prominent guidelines to estimate LoD from most prominent guidelines can be found in Table 1 (NB! For more specific overview of procedures, see the specific guideline!). These approaches can result in widely varying LoD estimates. Different guidelines often suggest different approaches and it is up to the analyst to choose which approach to use. If a specific approach is not demanded by the guideline, this choice must be made based on the necessities and properties of the analytical method.
An Excel sheet with example calculations of LoD with approaches in Table 1 can be found at the end of this chapter.
Table 1. Different approaches for determining LoD, CCα and CCβ.
|
Group |
Reference |
What is obtained? |
Equation |
|
1 |
[, , , ] |
LoD (considers and negative results – the probability of false positive and negative values depends on the choice of t) |
|
|
Description: Concentration of fortified samples in LoD range (e.g. lowest level where S/N > 3) or at maximum residue limit (); Assumptions, simplifications: ; Notes: Care must be taken when integrating blank samples; |
|||
|
2 |
[] |
LoD essentially equivalent to CCα (considers only false positive results) |
|
|
Description: A detailed procedure is given to choose fortified sample concentration (incl. estimating an approximate LoD first, measuring only 2 of the needed repeated samples before measuring the rest of the 7 samples); Assumptions, simplifications: Normal distribution of replicates; variability of the slope and intercept are not taken into account; Notes: LoD as equivalent to CCα ( results are not accounted for); |
|||
|
3 |
[] |
LoD (considers false positive and negative results – the probability of false positive and negative values depends on choice of t) |
|
|
Description: Second equation is used if LoD is estimated from single day measurement results and blank values are used for correction; Assumptions, simplifications: Homoscedasticity; normal distribution of the replicates;linearity of the calibration data; variability of the slope and intercept are not taken into account. Notes: Using (not standard deviation) to estimate LoD is suggested. |
|||
|
4 |
[] |
LoD (considers false positive and negative results) |
|
|
Description: Regression line must be in the range of LoD. Assumptions, simplifications: Homoscedasticity; Notes: The standard deviation of the intercept underestimates the variance of the results at 0 concentration and should not be used. |
|||
|
5 |
[, ] |
LoD (considers false positive and negative results) |
Cut-off approach: number of repeated measurements (usually 10) are made at different concentrations near LoD. The lowest concentration at which all the samples are „detected“ is used as the LoD. The detection threshold can be established for example based on the S/N, visual evaluation or automatic integration for chromatographic methods.
|
|
Assumptions, simplifications: Uses robust statistics. This approach does not assume normal distribution. Notes: This approach is very work intensive; |
|||
|
6 |
[, ] |
CCα and CCβ |
CCα: 1. Calculated as
|
|
Description: Some simple approaches suggested to estimate CCα and CCβ; Assumptions, simplifications: Notes: CCα and CCβ are found for minimum required performance level or MRL. |
|||
|
7 |
[] |
CCα and CCβ |
|
|
Description: Given equations are for homoscedastic data;
The blank measurements are required to also be included in the calibration points. Assumptions, simplifications: Normal distribution of the replicates; Notes: In this guideline the concentration scale is called the net state variable and the intensity scale is called the response variable. |
|||
Calculating CCα and CCβ
http://www.uttv.ee/naita?id=23348
https://www.youtube.com/watch?v=BQ_dOEMDoDs
Estimating CCα and CCβ
The approaches that are usually suggested to estimate CCα and CCβ are more complex than the approaches suggested for LoD. This is so because their definition is statistically more rigorous (demanding a known probability level of false positive and negative results) but the results are also more reliable. Some approaches to estimate CCα and CCβ suggested in the guidelines and articles can be found in Table 1.
The CCα and CCβ calculations [] take into account the standard deviation of the used linear regression line parameters (slope and intercept). This variance is propagated into the concentration values that are calculated by using these parameters. As CCα and CCβ are used in the concentration scale (similarly to LoD) the variance of the slope and intercept must be taken into account when estimating them.
Another property that must be considered is homo- and heteroscedasticity. Homoscedasticity means that the variance of signal is constant in case the concentration changes and heteroscedasticity therefore means that the variance changes with the concentration (see example in Figure 1). Analytical methods are often heteroscedastic – as the concentration increases, the standard deviation of the measurements also increases. If it is shown that the collected calibration data collected is heteroscedastic then, weighted linear regression (WLS) should be used to take the variance of the slope and intercept more accurately into account. A simplified approach that usually works sufficiently well is presented below.
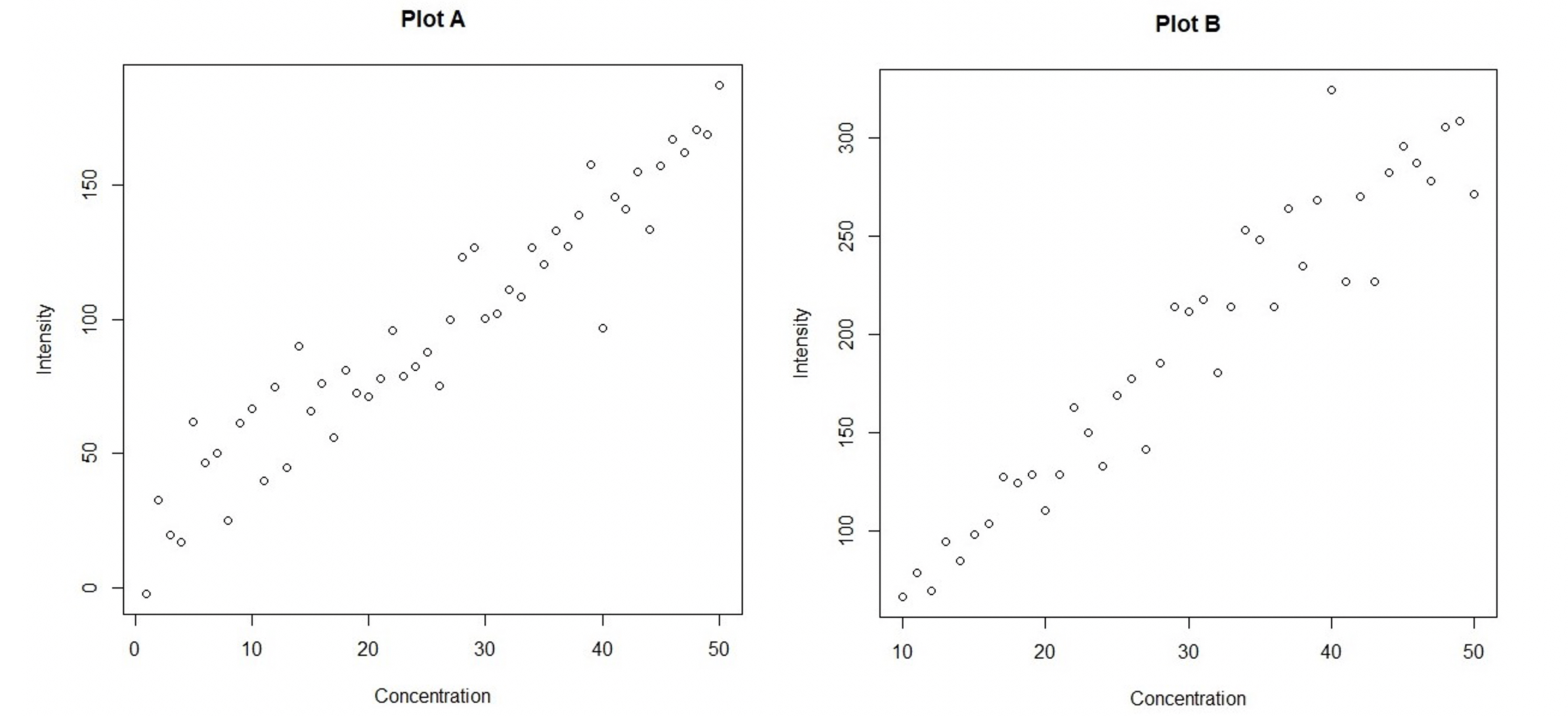
Figure 1. Data in Plot A are homoscedastic and data in Plot B are heteroscedastic. In plot A as the concentration increases the variability of results in intensity scale does not increase. However, in Plot B the variability of intensity values increases as the concentration increases.
With WLS the propagated errors of the slope and intercept to the concentration value significantly decrease at lower concentration levels. Therefore, the CCα and CCβ values are also significantly influenced. Using WLS can be complex and a possibility to avoid this is to select a narrow concentration range at lower concentrations from the calibration data that can be shown to be reasonably homoscedastic. These data can then be used to estimate the slope and the intercept with ordinary linear regression (OLS) which assumes that the data are homoscedastic. As a result calculating the CCα and CCβ estimates also becomes simpler.
Important aspects of estimating LoD and CCα, CCβ
http://www.uttv.ee/naita?id=23350
https://www.youtube.com/watch?v=9GFMa0AYkdA
It should be considered how important the LoD value for a given analytical method is. Based on this knowledge it can be chosen whether a simple approach to estimate a LoD is enough or a more complex approach that makes less assumptions (e.g. about homoscedasticity) and therefore gives more accurate results should be used. The important assumptions made by different approaches are summarized in Table 1. Further details about how to evaluate whether these assumptions can be made is discussed in the following references [, ]. If the analyte concentration will never come close to a LoD value then LoD does not have to be estimated at all. However, often LoD is still estimated in these cases just for proving that the samples are significantly above the LoD of the method. For example, when measuring calcium in milk by complexometric titration, we do not have to worry that in some samples the concentration of calcium might be so low that it would be below a LoD for a reasonable titration procedure. However, if the LoD estimate is an important parameter used to interpret the results of an analysis, more complex and accurate approaches must be used to estimate LoD. For example, when analyzing blood samples of athletes for doping, the method must interpret the results correctly even if only very small amounts of the analyte is detected. Therefore, CCα and CCβ values estimated with complex approaches that make less assumptions (e.g. ISO []) must be used.
In some cases the analytical method can have properties that do not allow the use of some LoD estimation approaches. For example, it can be difficult to estimate the standard deviation of the blank for LC-MS/MS methods as the noise can be zero due to the signal processing. As the blank values all give intensity of 0, the LoD value cannot be calculated from them but the standard deviation at 0 can be still estimated by other approaches: from the standard deviation of the intercept value or from the standard deviation of the residuals. A more thorough discussion about the problems of processing chromatograms of samples at low concentrations can be found in the following references [, ]. In conclusion, in general the analyst must understand which approaches cannot be used for a given analytical method.
It should always be kept in mind that LoD is an estimated value and never represents the true LoD as it is calculated from the parameters that deviate randomly from their true value between measurements. Moreover, the true value around which the results deviates can change randomly between days. For example, the slope of the LC-MS/MS changes significantly between days – this means that the true intensity value given by a concentration changes between days. For this reason, the within-day standard deviation is lower than the standard deviation of results collected on different days (see section 4.1). Therefore, LoD also changes between days. To take this fact into account, the LoD should be estimated over a long period of time (e.g. a month) and the median LoD value can then be used []. If it can be seen that the LoD estimate changes significantly between days (meaning the variation of LoD value within a day is significantly smaller than between days) and the estimate is important for the correct interpretation of the results on that day, then the LoD should be estimated on that day and that value should be used for the interpretation. However, it can also be noted here that if the LoD is used only for simple characterization of the method and not used further (see above), then the LoD does not have to be estimated on multiple days. It must also be noted that the previous discussion also applies for CCα and CCβ.
As the different approaches can give differently biased values, it should be always stated which approach is used to evaluate the LoD. If different approaches are used (to characterize the lab or the new method), then the comparison should be made with caution.
A different concept for estimating LoD is by using the signal-to-noise ratio (S/N). This approach is mostly used in chromatographic methods. Modern chromatography programs determine this value automatically. The signal value for this is found from the height of the peak and noise values are found from either the standard deviation of the noise or from so called peak-to-peak value (meaning the difference between the highest and lowest points in the noise). From this it can be seen that S/N can be found for only one measurement of a sample. A single measurement however does not take into account the variability between measurements and therefore the LoD should not be evaluated from this result. A scheme has been suggested by Eurachem where 10 samples are measured on different concentration levels and the lowest concentration where all 10 are detected is taken as the LoD. Here the decision that an analyte has been detected can be made from the fact that the S/N is equal to or over 3. However, this means that many measurements have to be made to estimate the LoD and due to the S/N being conceptually different from other approaches, it will be difficult to compare the LoD estimates found with other approaches.
Calculating LoD
http://www.uttv.ee/naita?id=24440
https://www.youtube.com/watch?v=u7LCGkFuUFE
In case you have trouble with LINESt function in excel, we recommend you to review the following video.


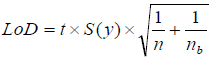 (Eq 4)
(Eq 4)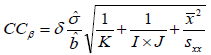 (Eq 9)
(Eq 9)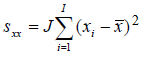 (Eq 10)
(Eq 10)