MOOC: Validation of liquid chromatography mass spectrometry (LC-MS) methods (analytical chemistry) course
10.4 Experimental design
Additionally to the One factor at a Time approach (OFAT, explained in 10.3), can also be estimated by varying multiple method parameters (factors) at the same time. Such approaches are strongly recommended if it is expected that different method parameters have interactions: meaning that the value of one parameter influences another value of a different parameter. In chromatography, the parameter interactions between some of the parameters are rather the rule than the exception []. Therefore, using OFAT can lead to getting only a partial and/or flawed picture of the method robustness. For example, the retention behaviour of the acidic compounds in RP is influenced by the mobile phase pH. Additionally, changing the additive concentration can at the same time strongly influence pH and, in turn, changing pH can influence the effect of the additive. These interactions will remain unnoticed with One factor at a Time approaches.
A statistical approach to validation procedures is the Design of Experiment (DoE). This tool has been broadly applied for many years in method optimization but is also relevant for the method validation process. Even though a DoE is not yet prominently illustrated in the validation guidelines for analytical method development, publications in recent years have shown [ and ] that it is on its way to becoming a valuable mainstream tool for evaluating robustness. Additionally, a DoE chapter has been added to the 10th version of the European Pharmacopoeia (Ph. Eur.) and will certainly influence the future of validation guidelines.
How to perform a DoE
Design of Experiment
https://www.uttv.ee/naita?id=32135
https://youtu.be/D71f9uFqHDA
The most basic way to study the robustness of a method is called full factorial design, carried out as in the following example for a robustness evaluation:
a) Brainstorm and list all factors which are likely to influence the robustness of a newly developed chromatographic method. The DoE approach is needed to determine if the factors like the eluent pH (let’s call it factor A), the additive concentration of the eluent (B) and the column temperature (C) have a critical impact on the retention time (also called response variable). The three factors (A, B and C) are set on two coded levels, a high (+) and a low level (-), which are depicted in the table below. We are using one level above and one below our optimal factor set to evaluate the robustness in both directions. The factor levels themselves are chosen by the chemist in charge of the validation and should be placed in a reasonable distance from the optimal factor setting. In practice, this means considering errors in laboratory work that appear while creating e.g. a new eluent solution and then predicting based on these thoughts ΔpH or ΔAdditive conc. values, which can be used as upper and lower levels in DoE.
To calculate the number of experiments at different factor combinations, a simple formula can be used:
 (Eq 1)
(Eq 1)
where n – number of experiments performed at different combinations
k – number of factors.
In the current example k = 3: pH, additive concentration, column temperature. Thus, we need to perform 8 experiments in total to determine the robustness of the response variables at two levels.
b) Construct a measurement plan that would contain all possible combinations of the factor levels for one substance in the mixture.
Note 1: We are monitoring the retention times of all analyte substances, so by performing the experiments later, we can create tables like the following ones for all substances which are planned to be separated in the mixture and calculate the specific effects for every substance individually.
Note 2: If is a concern to you then it is recommended to use a central point in DoE with only “optimal” setting and repeating this point multiple times at random in the experimental plan instead of repeating the whole design itself.
In a step-by-step manner:
First, notice that in the table, we first add + signs to half of the experiments of the first factor column (pH).
|
Experiment number |
A
|
B
Additive conc. |
C
Column Temp. |
|---|---|---|---|
|
1 |
+ |
|
|
|
2 |
+ |
|
|
|
3 |
+ |
|
|
|
4 |
+ |
|
|
|
5 |
– |
|
|
|
6 |
– |
|
|
|
7 |
– |
|
|
|
8 |
– |
|
|
Then we fill in the next factor by splitting the first factors + signs in half.
|
Experiment number |
A
|
B
Additive conc. |
C
Column Temp. |
|---|---|---|---|
|
1 |
+ |
+ |
|
|
2 |
+ |
+ |
|
|
3 |
+ |
– |
|
|
4 |
+ |
– |
|
|
5 |
– |
+ |
|
|
6 |
– |
+ |
|
|
7 |
– |
– |
|
|
8 |
– |
– |
|
And we do the same for the third (all other columns that remain).
|
Experiment number |
A
|
B
Additive conc. |
C
Column Temp. |
|---|---|---|---|
|
1 |
+ |
+ |
+ |
|
2 |
+ |
+ |
– |
|
3 |
+ |
– |
+ |
|
4 |
+ |
– |
– |
|
5 |
– |
+ |
+ |
|
6 |
– |
+ |
– |
|
7 |
– |
– |
+ |
|
8 |
– |
– |
– |
c) Behind all the + and – signs are factor levels that are used to carry out the experiments. The decoded factors for this Full Factorial Design can be seen in the table below. Practically this means in our example to perform 8 LC runs with 4 different eluent solutions and varying temperatures in the column compartment according to the decoded values in the table below. All experiments need to be carried out in a random order to prevent a on the response variable. The reason for this is that unknown factors might be aligned with each other if the experiments are not performed in random order. From those 8 runs we collect all the retention times of all substances in the mixture in order to determine the robustness individually for every analyte. It is always possible to use more response variables than just the one (retention time) depicted here in this example.
Now in this step, we perform all the experiments and transfer the results, in our case, the retention time, to the table.
|
Experiment number |
Actual order of measurement |
A
pH |
B
Additive conc. |
C
Column Temp. |
Response 1
Ret. Time |
|---|---|---|---|---|---|
|
1 |
3 |
9.8 |
5.2 |
31 |
8.31 |
|
2 |
4 |
9.8 |
5.2 |
29 |
8.10 |
|
3 |
2 |
9.8 |
4.8 |
31 |
7.24 |
|
4 |
5 |
9.8 |
4.8 |
29 |
7.43 |
|
5 |
6 |
9.4 |
5.2 |
31 |
8.32 |
|
6 |
7 |
9.4 |
5.2 |
29 |
8.92 |
|
7 |
1 |
9.4 |
4.8 |
31 |
9.84 |
|
8 |
8 |
9.4 |
4.8 |
29 |
9.93 |
d) Now it is time to calculate the actual effects of the three factors on the response variables. This is done by finding the average for the response at a high value (“+”) and subtracting the average of the response at the low value (“-”). In case of a retention time, we would have:
 (Eq 2)
(Eq 2)
Effect of the factor A on the response would be calculated as follows:
 (Eq 3)
(Eq 3)
This is now the effect that the change in pH has on the response variable retention time. This calculation can be performed in a similar manner for all factors A, B, C, and all interactions.
|
Results retention time [min] |
||
|---|---|---|
|
A |
B |
C |
|
pH |
Additive conc. |
Column Temp |
|
-1.48 |
-0.20 |
-0.17 |
From this depiction, it is clear that the pH value especially has the highest influence on the retention time, in the way that a decrease in pH increases the retention time of the analyte, which would imply that the method is not robust regarding a pH change of ± 0.2 pH units.
This can also be visualized in the following plot. By the slope, it is easily deductible that the impact of the pH on the response variable retention time is greater than the effect of the additive concentration in the eluent. In general, the steeper the slope is, the more impact a factor has on the response variable. The effect size describes the numeric influence of the factor on the response variable in the set design region and can be used to distinguish the importance of effects from the less important ones.
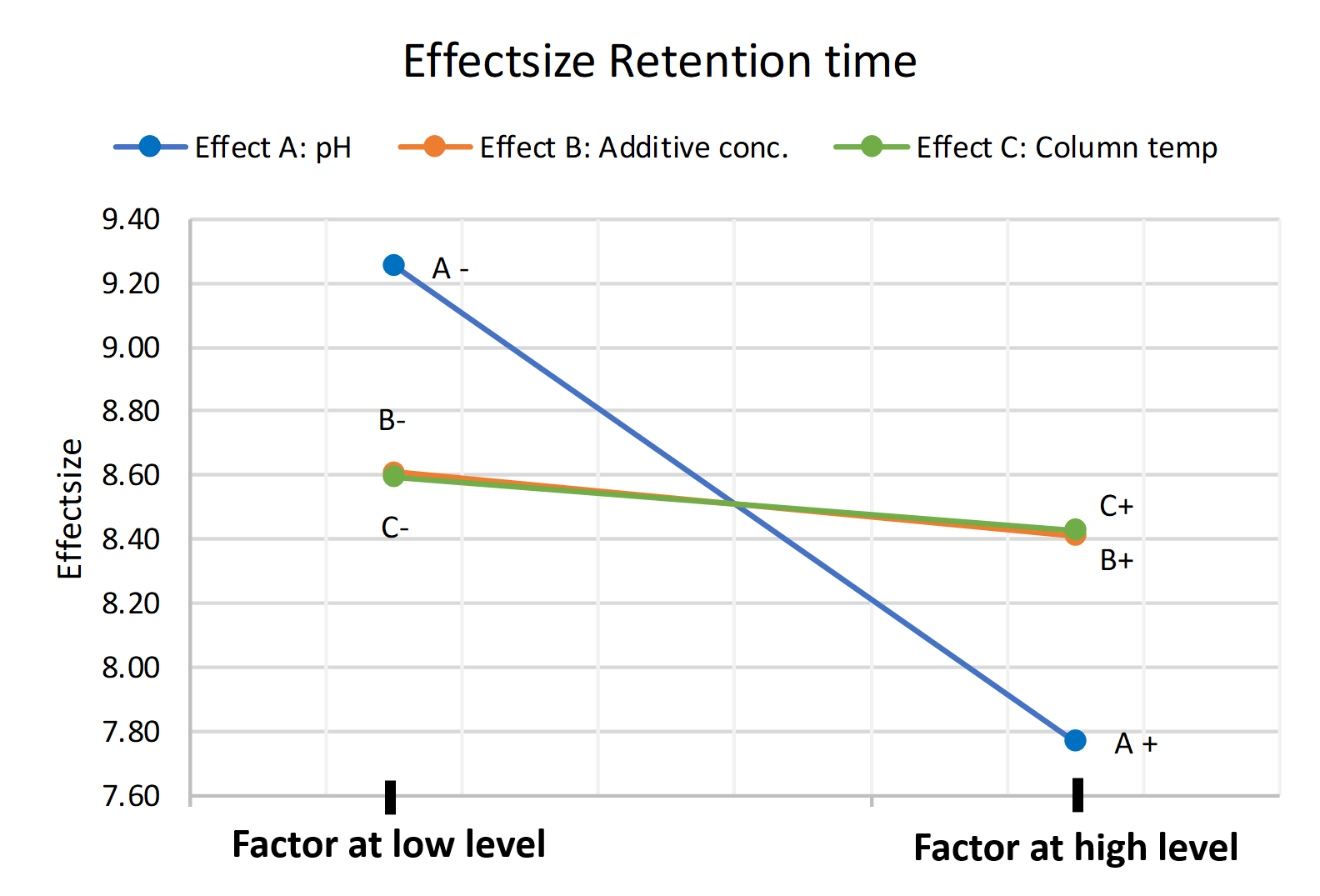
Figure 1 Main effect plot of pH, Additive conc. and Column temp. on the Retention time
The influence of the additive concentration in our chosen design region is less impactful on the retention time than pH change in our chosen design region on the retention time. Thereby, we might assume that the method is robust towards changes in additive concentration. But, as will be shown in the following section, this assumption would be wrong! In that’s section we will show the importance and benefits of also monitoring factor interactions instead of only the individual effects of the factors.
e) Interactions are important
One of the major advantages of a DoE approach is the determination of the effects of interactions on the response variable. To calculate these interactions, we proceed the same way as with the normal factors A, B and C. The coded value for an interaction is deducted by the multiplication of the single effects meaning that AB= A*B which might look like this
+ * + = + or this + * – = -.
So, for the interaction of AB (pH and additive conc.), we get coded values like this:
If we do the multiplication for all the interaction combinations, it creates the following table with the interactions.
|
Experiment |
AB |
BC |
AC |
ABC |
Ret. Time |
|---|---|---|---|---|---|
|
1 |
+ |
+ |
+ |
+ |
8.31 |
|
2 |
+ |
– |
– |
– |
8.10 |
|
3 |
– |
– |
+ |
– |
7.24 |
|
4 |
– |
+ |
– |
+ |
7.43 |
|
5 |
– |
+ |
– |
– |
8.32 |
|
6 |
– |
– |
+ |
+ |
8.92 |
|
7 |
+ |
– |
– |
+ |
9.84 |
|
8 |
+ |
+ |
+ |
– |
9.93 |
Now the effects of the interactions can be calculated with the same formula from above.
We can calculate the interaction effect the same way we calculated the single factor effect:
 (Eq 4)
(Eq 4)
 (Eq 5)
(Eq 5)
Now we have the complete picture of all effects on the response variable.
|
Results (factor and interaction effect sizes) For retention time |
||||||
|---|---|---|---|---|---|---|
|
A |
B |
C |
AB |
BC |
AC |
ABC |
|
pH |
Additive conc. |
Column Temp. |
pH * Additive conc. |
Additive * Column Temp. |
pH * Column Temp. |
pH * Additive * Column Temp. |
|
-1.48 |
-0.20 |
-0.17 |
1.07 |
-0.03 |
0.18 |
0.23 |
The two-factor interaction between a pH and an additive concentration has a big influence on the retention time. This implies that our method is not yet robust towards pH and additionally towards additive concentration. In our case, the conclusion comes from the comparison of numeric values of the effect size with each other. There is strong evidence towards the significance of pH and pH*Additive conc. However, easy identification of significant effects is not always given, and in these cases, it is strongly recommended to use an ANOVA approach to determine which effects and factors are statistically significant. A good ANOVA description in the context of a DoE can be found in the book []. However, all results from a DoE should always be evaluated from a practical scientific standpoint.
In general, it is assumed that the importance of interactions will decrease with additional interacting factors, so it is unlikely that there will be very significant (three), four or five-factor interactions.
Reaching this conclusion is only possible with the help of a DoE. If the user would use the OFAT approach, the effects of the interactions on the response variables would go completely unnoticed. Only with the application of a DoE we were able to see the impact of the two-factor interaction on the response variable.
Another way of portraying interactions is with the following plots. In both plots one factor is kept constant while the other factor is compared on its influence on the response variable. The plots firstly show us that there is an interaction between factor A and B because the slope changes visibly when only one factor is changed. Secondly, we can say that the interaction of AB is more influenced by the -1 setting for B than by the +1 setting of B.
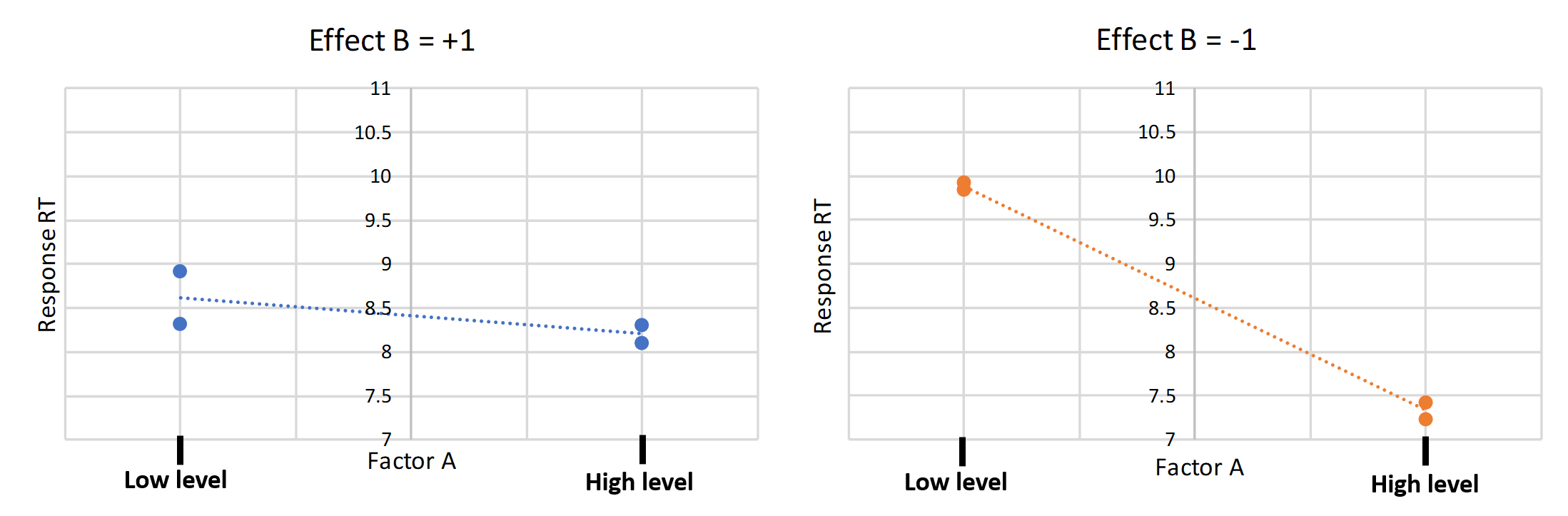
Figure 2 Interaction plots of the factors (A) pH and (B) Additive conc.
f) contour plots
A different way for the interpretation of the interactions on the response variable are the so-called contour plots, as seen in the figures below. These pots have been calculated and plotted in the “R” software with the packages pid and rsm. The lines in the plot depict the interaction between pH and additive concentration and their effect on the response variable. The black dots in the corners of the contour plot describe the design space where the measurement points have been set. The more the lines are bent, the stronger is the interaction. The examples make this evident. When looking at the figure of pH and additive concentration, we see strongly bent lines in the chosen design space, and therefore we can assume a strong interaction between the two factors. On the contrary, if we look at the interaction between pH and column temperature, then we only see a very weak interaction between those factors.
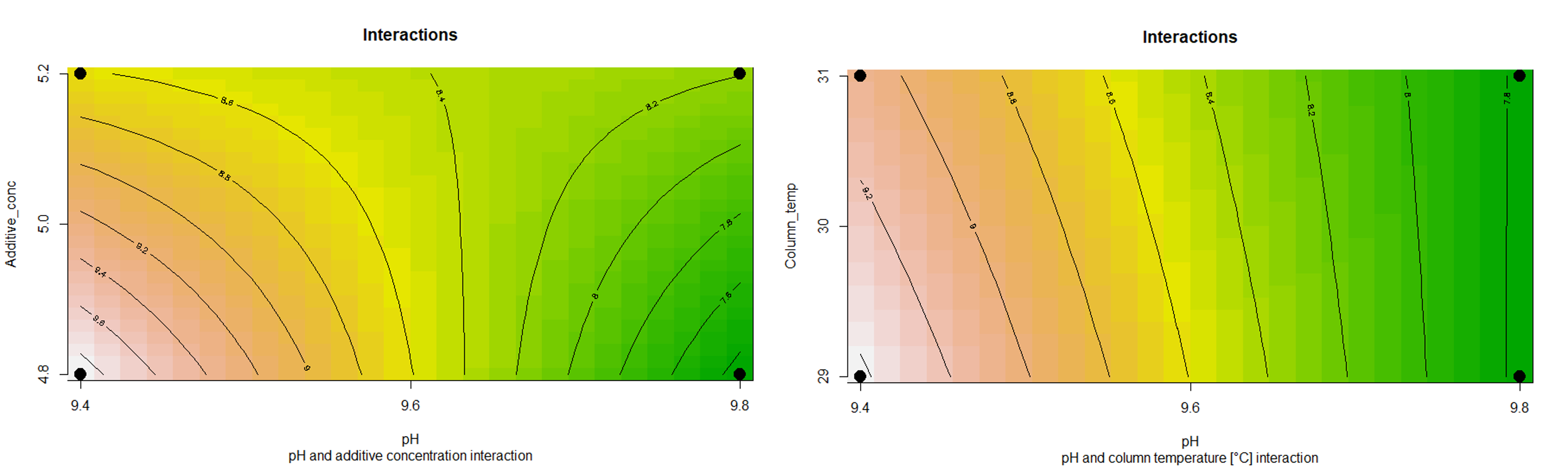
Figure 3 Contour plots of the interactions


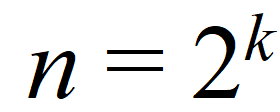
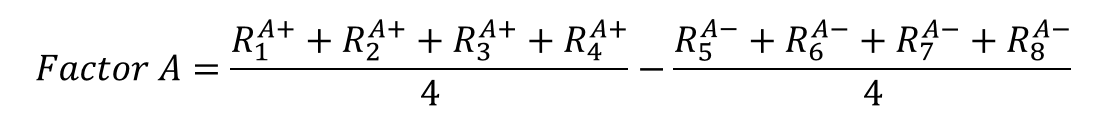 (Eq 2)
(Eq 2)
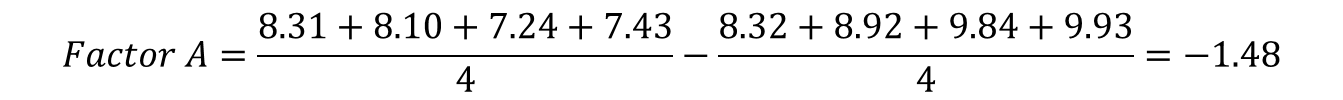 (Eq 3)
(Eq 3)
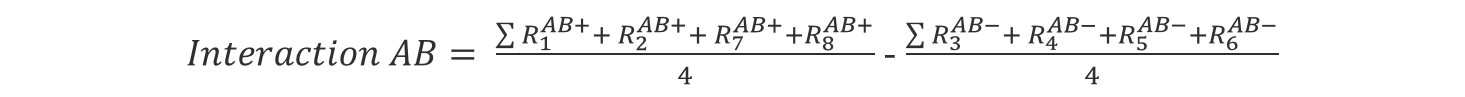 (Eq 4)
(Eq 4)
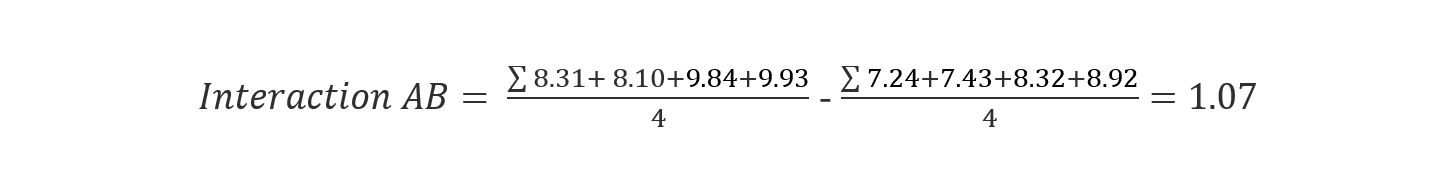 (Eq 5)
(Eq 5)