MOOC: Validation of liquid chromatography mass spectrometry (LC-MS) methods (analytical chemistry) course
4.2. Calculation of precision
Evaluation of requires a sufficient number of replicate measurements to be made on suitable materials. The materials should be representative of the test samples in terms of matrix and analyte concentration, homogeneity and , but do not need to be Certified Reference Materials (CRMs). The replicates should be independent, i.e. the entire measurement process, including any sample preparation steps, should be repeated. The minimum number of replicates varies in different validation guidelines, but is typically between 6 and 15 for each of the material used in the study.
Precision is usually expressed as “imprecision”: absolute standard deviation (s) (Eq 1), relative standard deviation (RSD) (Eq 2), variance (s2) or coefficient of variation (CV) (same as RSD). Importantly, precision is not related to the reference values.
 (Eq 1)
(Eq 1)
 (Eq 2)
(Eq 2)
s – standard deviation
n – number of measurements made
xi – each measurement result
xmean – mean value of the measurement results.
It is not possible to estimate a reliable standard deviation from data sets with few replicate measurements. If acceptable, the values calculated from several small sets of replicate measurements can be combined (pooled) in order to obtain estimates with sufficient number of degrees of freedom. The pooled standard deviation is calculated with Eq 3 or with Eq 4, if the number of measurements made with each sample is the same. Pooled standard deviation is useful if for some reason it is impossible to make a sufficient number of replicates with one sample – either because of the time constraints (e.g. stability) or because the available amount of sample is insufficient for replicates. Standard deviations can also be pooled when the same analyte is determined in different samples. However, in this case the samples should be reasonably similar (but not necessarily identical) in terms of the analyte content and matrix.
 (Eq 3)
(Eq 3)
 (Eq 4)
(Eq 4)
k – number of samples
s1, s2 etc – sample standard deviations
n1, n2 etc – number of measurements made for different samples
General formula for the case when the experiment is done with different samples, each measured on a single day:
 (Eq 5)
(Eq 5)
k – number of groups (in this case samples)
RSD1, RSD2, etc – within group standard deviations
n1, n2, etc – numbers of measurements made for different samples
Pooled standard deviation is a weighted root mean square (RMS) average of standard deviations, whereby numbers of degrees of freedom of the individual standard deviations serve as weights.


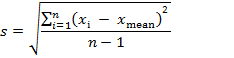 (
(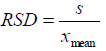 (Eq 2)
(Eq 2)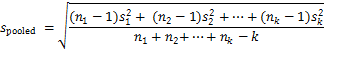 (
(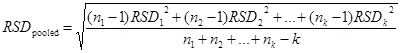 (Eq 5)
(Eq 5)