2. Lokaliseerimine

Kuidas käib roboti lokaliseerimine?

Robot ei saa kunagi oma maailmatajus kindel olla, sest nagu füüsikatunnist mäletame, siis iga mõõtmine sisaldab määramatust. Ent robot tajub oma maailma ainult läbi eri andurite ehk mõõteseadmete. Seetõttu on robot alati ebakindel, eriti kui ülesandeks on tema enda asukoha määramine keskkonnas.

Isegi kui suudame roboti hetke asukoha täiuslikult määrata, tekivad kirjeldatud probleemid kohe uuesti, kui robot liigub. Mida kauem robot liigub, seda suurem on andurite määramatusest tingitud ebatäpsus ning seda ebakindlamad saame olla roboti asukohta hinnates. Ent siin tuleb meile appi matemaatika, mis võimaldab siduda roboti anduritest saadud lugemid ja nende lugemite usaldusväärsuse, et võimalikult täpselt hinnata roboti asukohta.

Näiteks kujutame ette olukorda, kus meie robot saab olla ainult ühes neljast allpool joonistatud ruudust. Kuigi me ei tea täpselt, millises alas robot asub, saame siiski omistada igale ruudule mingisuguse tõenäosuse, et robot just selle ruudus asub. Alloleval joonisel on näitlikustatud, kuidas saame taolisi tõenäosusi graafiliselt esitada (antud juhul on siis kõige suurem tõenäosus, et robot asub ruudus 3).

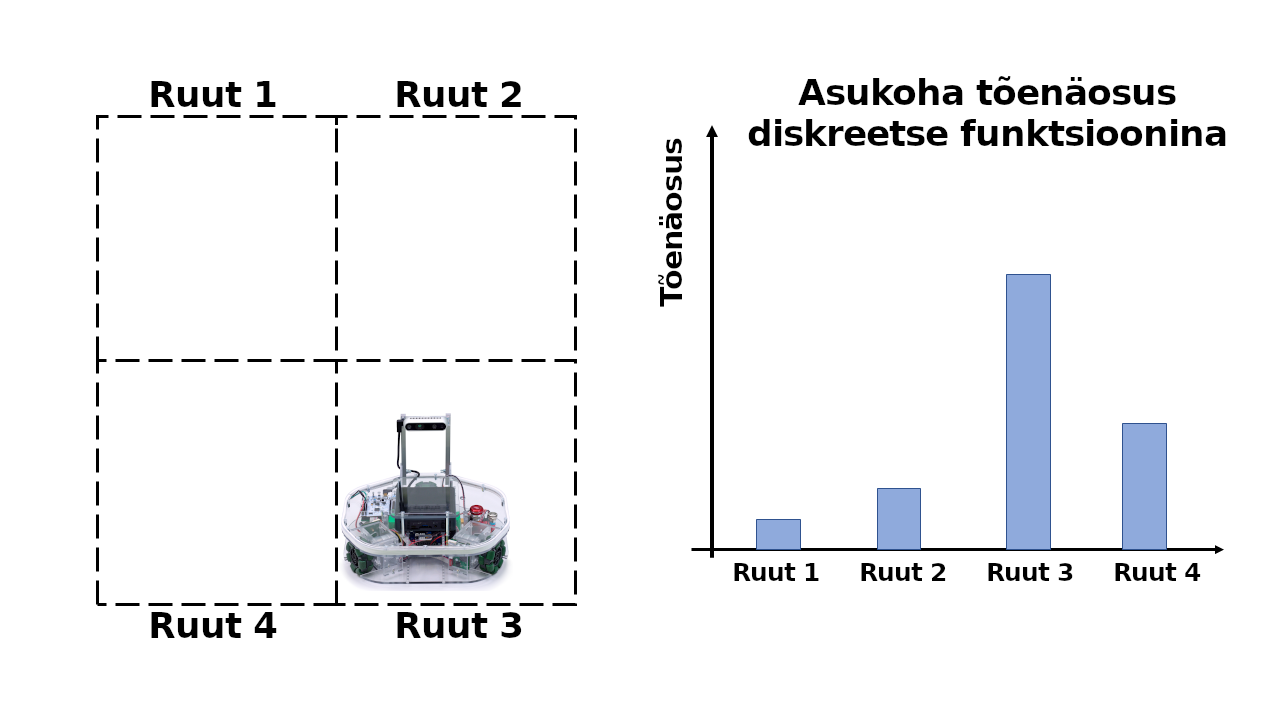
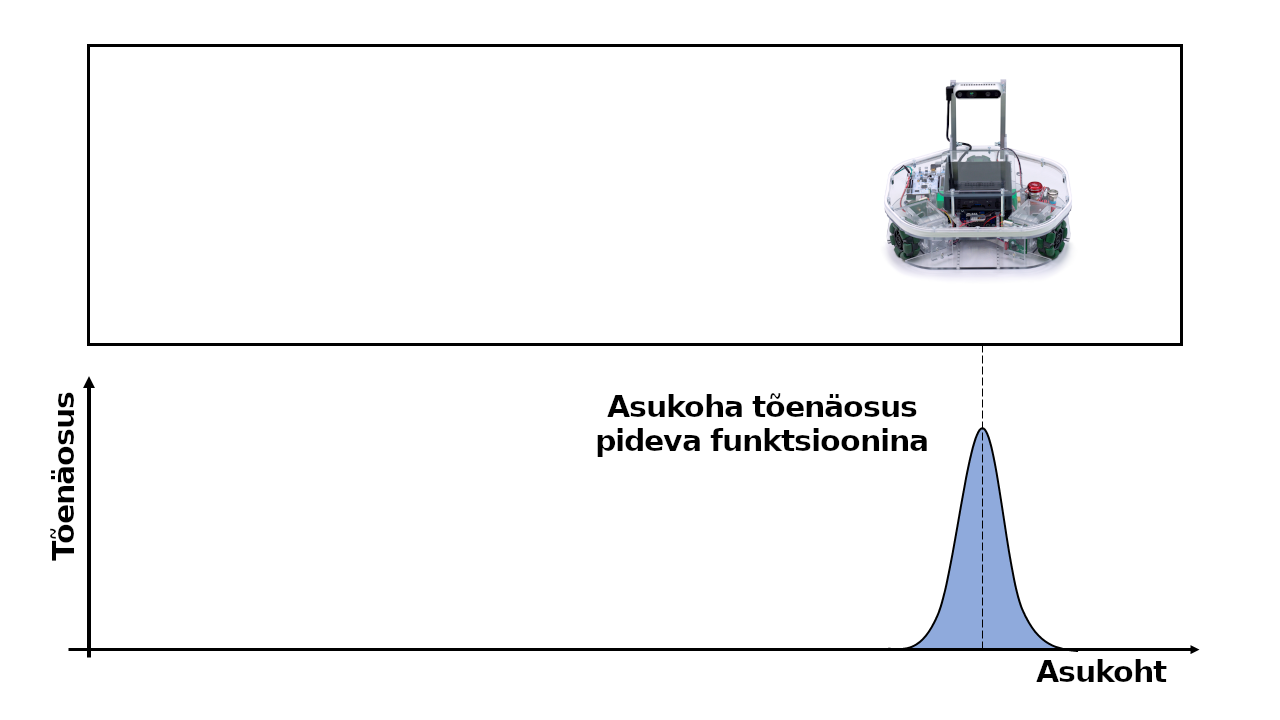
Tihti aga kasutame robotite asukoha tõennäosuse kirjeldamiseks mitte tabelit/diagrammi, kust saame välja lugeda ühe väärtuse konkreetse lahtri kohta, vaid kirjeldame roboti asukoha hoopis pideva funktsiooni abil nagu alljärgneval pildil. Taoline matemaatiline funktsioon võimaldab, et meil mistahes ruumipunkti kohta öelda, kui suure tõenäosusega robot seal asub. Mida kitsam on meie roboti asukohta kirjeldav tõenäosusfunktsiooni kõver, seda kindlamad saame olla robot asukohas.

Selles harjutuses on kasutatud ja mugandatud David Kostolani (TU Wien) loodud õppematerjale.