2. Asend ja kinemaatika

Liigendid võimaldavad roboti lülidel olla erinevates positsioonides ja orientatsioonides. Lüli positsioon on selle asukoht ruumis; orientatsioon on lüli pööratuse suund ja kaugus. Koos moodustavad need lüli asendi (ingl k. pose).

Positsioon + orientatsioon = asend

Tüüpiline jadamanipulaatori kasutamise ülesanne on selle mõjuri õigesse asukohta viimine. Seda asukohta saab kirjeldada erinevates koordinaatsüsteemides. Enimtuntud koordinaatsüsteem on ruumikoordinaadid (ingl k. Cartesian space), milles asukohta kirjeldatakse x-, y- ja z-teljes.

Selles kolme ristuva teljega kolmemõõtmelises ruumis on lihtne kirjeldada suvalise punkti asukohta. Samuti on selles koordinaatsüsteemis lihtne määrata manipulaatori mõjuri asukohta.

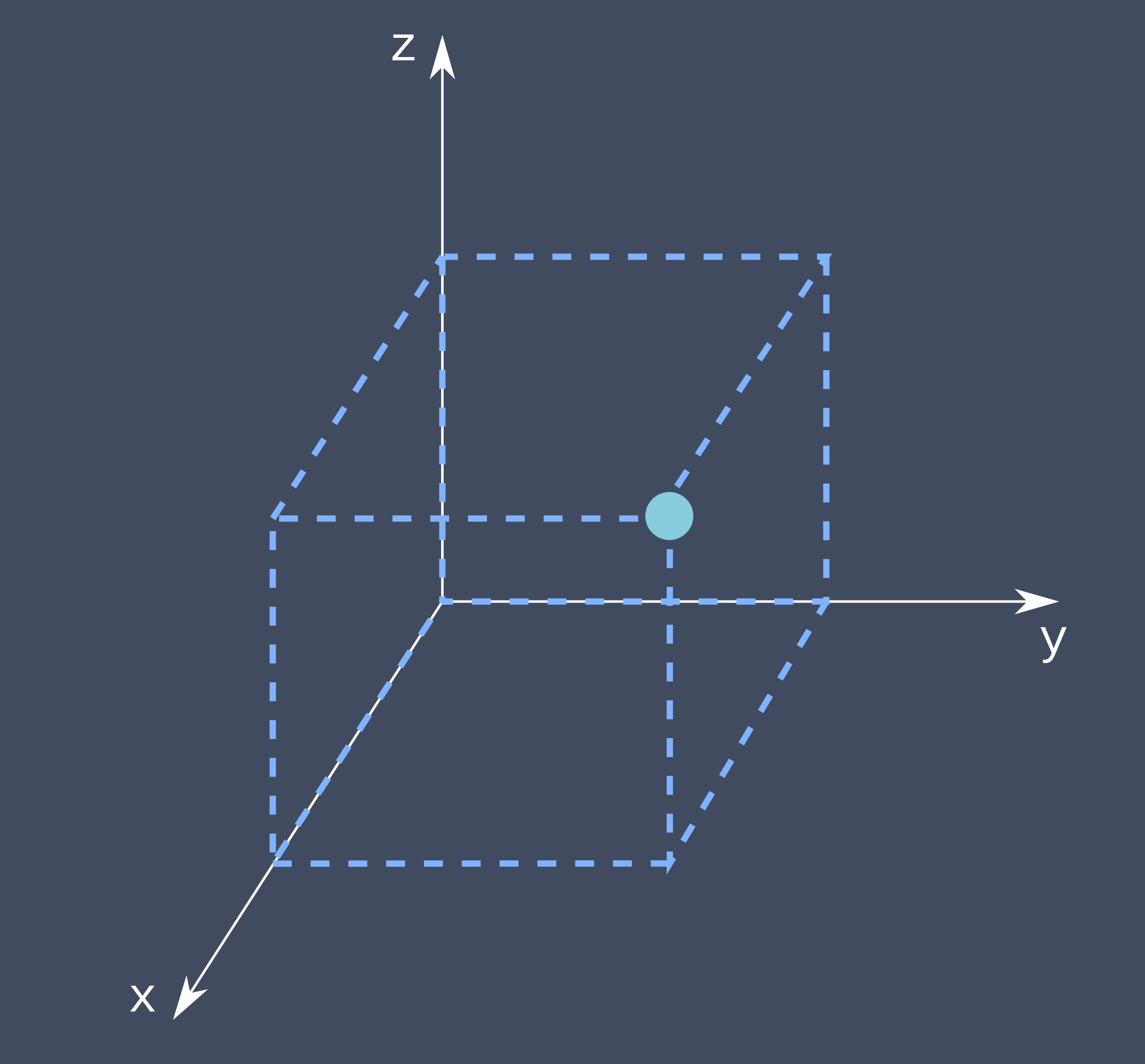
Kui valime manipulaatori mõjuri asukoha ruumikoordinaatides, siis määrame me ainult roboti ühe osa kohta positsiooni, aga mitte kogu roboti asendi. Kui soovime kirjeldada roboti kõigi lülide asendit, peame määratlema rohkem punkte. Piisab, kui kirjeldame iga liigendi asendi, selle asemel, et määrata kõigi lülide asukohta.

Kui teame jadamanipulaatori iga pöördliigendi nurka, saame üheselt kirjeldada roboti iga osa asendit. Seda liigendite nurkade kogumit nimetatakse liigendi olekuks (ingl k. joint state). Liigendi olekut teades on võimalik taasluua kogu roboti asend.

Kõigi võimalike liigendiolekute kogumit nimetatakse liigendiruumiks (ingl k. joint space).

Liigendiruumis on meil info iga liigendi nurga kohta. Kui teame, millised lülid iga liigendi külge ühenduvad, saame teada, milline on iga lüli suhteline asend sellega ühendatud lülide suhtes. Teoorias saame selle järgi leida manipulaatori mõjuri asendi, aga kuidas?

Selle jaoks on pärikinemaatika (ingl k. forward kinematics). Pärikinemaatikat ja roboti kirjeldust kasutades saame viia info liigendiruumist koordinaatruumi. Näiteks teades liigendiolekut saame arvutada manipulaatori mõjuri asendi koordinaatruumis. Pärikinemaatika on üsna lihtne ja kasutab tavalist trigonomeetriat. Tavaliselt tehakse neid arvutusi maatriksite korrutamise abil.

Tihti on robootikutel vaja lahendada pärikinemaatikale vastupidine ülesanne. Näiteks võib meil olla vaja viia roboti haarats järgmise eseme haaramiseks sobivasse asukohta. Eseme asukoht on kirjeldatud koordinaatruumis ja meil on vaja seada roboti liigendid õigete nurkade alla.

Oletame, et me teame, kuhu meil on vaja viia roboti mõjur. Meil on vaja seada kõik roboti liigendid ja lülid selliselt, et mõjur jõuaks vajalikku punkti. See tähendab, et meil on vaja leida liigendiruumist selline liigendiolek, kus roboti mõjur on soovitud koordinaatruumi punktis. Info viimine koordinaatruumist liigendiruumi ongi pöördkinemaatika (ingl k. inverse kinematics).

Pöördkinemaatika rakendamisel tekivad mõned probleemid. Soovitud asukohta jõudmiseks võib robotil olla vaja keerata ennast veidratel viisidel, mida ei ole lihtne arvutada. Me ei saa isegi olla kindlad, kas roboti mõjuril on füüsiliselt võimalik soovitud koordinaatidele jõuda. Ja mis juhtub, kui liigendiruumis on soovitud punkti jõudmiseks mitu erinevat liigendiolekut? Erinevalt pärikinemaatikast on pöördkinemaatika arvutuslikult keeruline ülesanne.

Õnneks on pöördkinemaatika rakendamiseks olemas mitmeid tarkvaralisi lahendusi.