4.2. Calculating the combined standard uncertainty

The uncertainty components that were quantified in the previous lecture are now combined into the combined standard uncertainty (u_c) – standard uncertainty that takes into account contributions from all important uncertainty sources by combining the respective uncertainty components. The concept of indirect measurement – whereby the value of the output quantity (measurement result) is found by some function (model) from several input quantities – is introduced and explained. The majority of chemical measurements are indirect measurements. The general case of combining the uncertainty components into combined standard uncertainty as well as several specific cases are presented and explained.

The first video lecture explains in a simple way how the uncertainty components are combined in the particular example of pipetting. The second video lecture presents the general overview of combining the uncertainty components.

Combining the uncertainty components into the combined standard uncertainty in the case of pipetting
http://www.uttv.ee/naita?id=17556

https://www.youtube.com/watch?v=S5v58VQ4zSg

In all cases where combined standard uncertainty is calculated from uncertainty components all the uncertainty components have to be converted to standard uncertainties.

In the example of pipetting the combined standard uncertainty is calculated from the uncertainty components found in the previous section as follows:

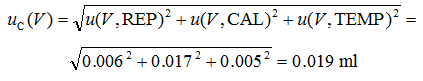(4.4)

This is the typical way of calculating combined standard uncertainty if all the uncertainty components refer to the same quantity and are expressed in the same units. It is often used in the case of direct measurements – measurements whereby the measurement instrument (pipette in this case) gives immediately the value of the result, without further calculations needed.

  Combining the uncertainty components into the combined standard uncertainty: simple cases and the general case
http://www.uttv.ee/naita?id=17826

https://www.youtube.com/watch?v=FJ4hn9LgGmw

An indirect measurement is one where the output quantity (result) is found ba calculation (using a model equation) from several input quantities. A typical example is titration. In case of titration with 1:1 mole ratio the analyte concentration in the sample solution C_S (the output quantity) is expressed by the input quantities – volume of sample solution taken for titration (V_S), titrant concentration (C_T) and titrant volume consumed for titration (V_T) – as follows:

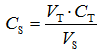(4.5)

In the general case if the output quantity Y is found from input quantities X₁, X₂, … X_n according to some function F as follows

(4.6)

then the combined standard uncertainty of the output quantity u_c(y) can be expressed via the standard uncertainties of the input quantities u(x_i) as follows:

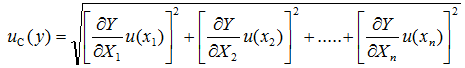(4.7)

The terms 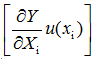  are the uncertainty components. The terms are partial derivatives. At first sight the eq 4.7 may seem very complex but it is in fact not too difficult to use – the uncertainty components can be calculated numerically using the Kragten’s spreadsheet method (as is demonstrated in section 9.7).

In specific cases simpler equations hold. If the output quantity is expressed via the input quantities as follows

(4.8)

then

(4.9)

                                

Importantly, irrespective of whether the input quantities are added or subtracted, the squared standard uncertainties under the square root are always added.

This way of combining uncertainty components is in principle the same as used above for the case of pipetting.

If the measurement model is

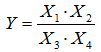(4.10)

then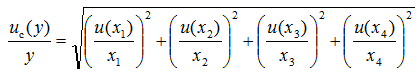

(4.11)

As can be seen, here it is the relative standard uncertainties that are combined and the squared summing gives us the relative combined standard uncertainty of the output quantity. The absolute combined standard uncertainty of the output quantity is found as follows:

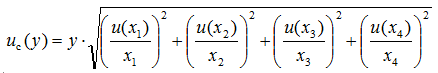(4.12)

The file used in second video can be downloaded from here.