4.1. Quantifying uncertainty components

Brief summary: The same pipetting as in lecture 2 is now examined from the point of view of quantifying the uncertainty sources. All the important sources of uncertainty are quantitatively expressed as uncertainty components – uncertainty estimates quantitatively describing the respective uncertainty source. The uncertainty components are quantified. An example is given on converting an uncertainty estimate with (assumedly) rectangular distribution into a standard uncertainty estimate.

Introduction to quantifying measurement uncertainty 
http://www.uttv.ee/naita?id=17555

https://www.youtube.com/watch?v=CaYJGxtQBzo

The main uncertainty sources are the same as explained in lecture 2 and here the uncertainty components corresponding to them are quantified.

• Uncertainty due to the non-ideal repeatability, which in the case of pipetting means that however carefully to fill and empty the pipette, we will nevertheless every time get a slightly different pipetted volume. Repeatability is a typical random effect. The standard uncertainty due to repeatability u(V, REP) can be calculated as standard deviation [1] of accurate volumes delivered by the pipette. [2]. According to the data for the used pipette is

(4.1)

• Uncertainty due to calibration of the volumetric equipment (often called calibration uncertainty or uncertainty of the nominal volume). This is the uncertainty in the positions of the marks on the volumetric ware. In the case of a given pipette it is a typical systematic effect. Calibration uncertainty of the pipette used in this example is specified by the producer as ± 0.03 ml. [3]   There is no information on the distribution or coverage of this uncertainty estimate. This is very common if uncertainty estimates are obtained from instrument documentation. In such case it is the safest to assume that the uncertainty estimate corresponds to rectangular distribution. In order to carry out uncertainty calculation we have to convert this uncertainty to standard uncertainty. For doing this, as explained in section 3.5, we have to divide it by square root of 3:

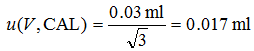(4.2)

• Uncertainty due to the temperature effect (often called as temperature uncertainty). All volumetric ware is usually calibrated at 20 °C and volumes usually refer to volumes at 20 °C [4]. Temperature change affects first of all the density of the liquid (the effect of expansion/contraction of glass is significantly smaller). If pipetting is done at a higher temperature than 20 °C then there amount of liquid (in terms of mass or number of molecules) pipetted is smaller than corresponds to the volume at 20 °C. Consequently, the volume of that amount of liquid at 20 °C is also smaller than if the pipetting were done at 20 °C. If the temperature of the laboratory and, importantly, temperature of the pipetted liquid, is constant during repeated measurements then the temperature effect is a systematic effect. The following video explains calculating the standard uncertainty of liquid volume due to the temperature u(V, TEMP):

u(V, TEMP) is dependent on the volume V of liquid delivered, [5] the maximum possible temperature difference from 20°C (Δt) and the thermal expansion coefficient of water γ. It is calculated as follows:

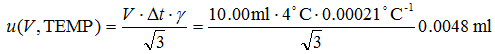(4.3)

Dividing by square root of 3 is for transforming the uncertainty estimate into standard uncertainty (assuming rectangular distribution of Δt). It is important to note that the V in eq 4.3 always refers to the actual measured volume, not the full capacity of the volumetric device. For example, if 21.2 ml of solution was measured with a 50 ml burette then the volume to use is 21.2 ml, not 50 ml.

In the case of more complex uncertainty estimations some of the sources can be presented also with expanded uncertainty. For example, the analyte content in reference material: (0.2314 ± 0.0010) mg/kg, k=2.  In this case this uncertainty also needs to be converted to standard uncertainty for further calculations. For that the expanded uncertainty is divided by the presented coverage factor.  So in the given example the combined standard uncertainty is 0.0005 mg/kg.

***

[1] Since pipetting for delivering a certain liquid volume is done only once and cannot be averaged (i.e. it is not possible to pipet several times and then “average” the volumes) the suitable estimate of repeatability uncertainty is the standard deviation of a single measurement, not standard deviation of the mean.

[2] The accurate volumes can be measured by weighing the water delivered by the pipette and converting it into volume by using accurate density data.

[3] This uncertainty can be significantly reduced if the pipette is recalibrated in laboratory by weighing the delivered water.

[4] If volumetric glassware is calibrated in the same laboratory then a different temperature can be used.

[5] In the case of a volumetric pipette the nominal volume is the same as the delivered volume but in the case of a burette it is usually not. So, if from a 25 ml burette 12.63 ml of solution is delivered then the volume that has to be used for temperature effect calculation is 12.63 ml, not 25 ml.