An analyst determined nitrate concentration in cucumber using potentiometry with ion-selective electrode (ISE).
She prepared calibration solutions from a high-purity (uncertainty due to purity can be assumed negligible) standard substance (KNO3) and conditioning solution (1% Na2SO4 solution), which was used for filling the flask to the mark, and carried out calibration of the electrode. The concentrations and electromotive force (EMF) readings of the calibration solutions were the following:
| Ci(NO3–) (mol/l) |
Ei (mV) |
| 0.1 |
179 |
| 0.01 |
237 |
| 0.001 |
295 |
| 0.0001 |
351 |
Calibration graph is prepared as E vs logC (using logarithm of concentration is common in potentiometry). The formal (see below for the model for actual calculations) calibration equation is:
E = E0 + b1 · logC (1)
The standard uncertainties of the calibration graph slope b1 and intercept E0 can be assumed equal to their standard deviations as found from regression analysis (e.g. using the LINEST function as is done in the calculation example of section 9).
The cucumber sample was carefully homogenized, the resulting slurry was transferred to a VFlask = 100 ml volumetric flask, which was weighed before and after the transfer. The uncertainty of the volumetric flask volume (taking into account all uncertainty sources) is ± 0.05 ml. From the mass difference the sample mass was determined as mSample = 9.167 g. The standard uncertainty of this mass (taking into account all uncertainty sources) can be estimated as 0.002 g. The volumetric flask was filled to the mark with the conditioning solution. It is expected that part of the nitrate may be lost during the process, which is taken into account by recovery correction. The recovery in this case can be estimated as R = 0.95 with standard uncertainty 0.05.
The sample solution was measured with the same measurement system as the calibration solutions and the reading ESample = 341 mV was obtained for the sample solution. Its uncertainty can be estimated as ±2 mV, which covers all uncertainty sources, except interference from chloride ions. Chloride ions are the main interference when measuring nitrate with ion-selective electrode. Chloride content in the sample is not measured but is estimated as CCl_Sample = (40 ± 30) mg/100g. This is a very approximate estimate, which is expected to cover the possible chloride contents in almost all vegetables. The selectivity coefficient of the electrode with respect to chloride is KSel_Cl = (0.005 ± 0.003). The selectivity coefficient value 0.005 means that the electrode is 200 times more sensitive to nitrate than to chloride.
The EMF of the sample solution is dependent on the concentrations of nitrate and chloride ions in the sample solution in the following way:
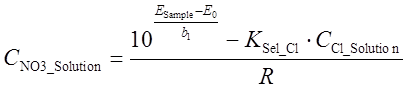 (2)
(2)
From here CNO3_Solution can be expressed as follows:
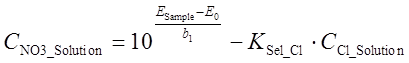 (3)
(3)
Please note that CNO3_Solution is only the concentration of nitrate ion (expressed in mol/l) in the sample solution. In order to obtain nitrate content in the sample (expressed as mg/100g) additional calculations are needed, taking into account the sample mass, volumetric flask volume and molar mass of NO3– (62.01 g/mol), as well as the recovery R. Furthermore, before calculating with eq 3, CCl_Solution has to be found from CCl_Sample using the sample mass, volumetric flask volume and molar mass of Cl– (35.45 g/mol). The uncertainty of molar masses is negligible. The extraction recovery of chloride can be considered 1.
On the basis of these data, please find nitrate content in the cucumber expressed in mg/100g, as well as its k = 2 expanded uncertainty.



