
Estimation of measurement uncertainty in chemical analysis
2. The origin of measurement uncertainty
Brief summary: Explanation, on the example of pipetting, where measurement uncertainty comes from. The concept of uncertainty sources – effects that cause the deviation of the measured value from the true value – is introduced. The main uncertainty sources of pipetting are introduced and explained: repeatability, calibration, temperature effect. Explanation of random and systematic effects is given. The concept of repeatability is introduced.
The first video demonstrates how pipetting with a classical volumetric pipette is done and explains where the uncertainty of the pipetted volume comes from.
Why measurement results have uncertainty? The concept of uncertainty source explained on the example of pipetting
http://www.uttv.ee/naita?id=17577
https://www.youtube.com/watch?v=ufWJB9orWdU
The second video demonstrates pipetting with a modern automatic pipette and explains the uncertainty sources in pipetting with an automatic pipette [1] .
Measurement uncertainty sources of pipetting with an automatic pipette
http://www.uttv.ee/naita?id=18164
https://www.youtube.com/watch?v=hicLweJcJWY
Measurement results have uncertainty because there are uncertainty sources (effects that cause uncertainty). These are effects that cause deviations of the measured value from the true value. [2]These sources also cause the existence of error and could therefore also be called error sources. If the used measurement procedure is well known then the most important uncertainty sources are usually also known. Efforts should be made to minimize and, if possible, eliminate uncertainty sources by optimizing the measurement procedure (analysis procedure). The uncertainty sources that cannot be eliminated (and it is never possible to eliminate all uncertainty sources) have to be taken into account in uncertainty estimation.
The magnitudes of the deviations caused by uncertainty sources are usually unknown and in many cases cannot be known. Thus, they can only be estimated. If we can estimate the magnitudes of all important uncertainty sources then we can combine them and obtain the estimate of measurement uncertainty, which in this case will be called combined measurement uncertainty. How this combining is mathematically done, will be demonstrated in the coming lectures.
If we make a number of repeated measurements of the same measurand then ideally all these repeated measurements should give exactly the same value and this value should be equal to the true value of the measurand. In reality the results of the repeated measurements almost always differ to some extent and their mean value also usually differs from the true value. The uncertainty sources cause this. In a somewhat simplified way the uncertainty sources (or effects) can be divided into random effects and systematic effects. [3]It is in principle not wrong to call them random and systematic sources of uncertainty, but this is not usually done. This is largely because, as we will see in a coming lecture, the concept of measurement uncertainty stresses that random and systematic effects should be treated the same way. The following scheme illustrates this (green circles denote true values, yellow circles denote measured values):
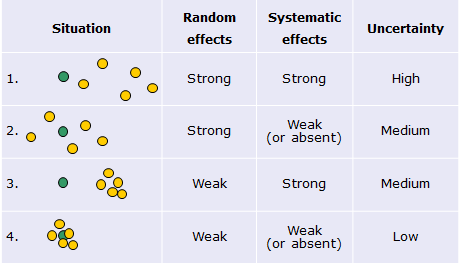
Scheme 2.1. The influence of random and systematic effects on measurement uncertainty.
Random effects cause the difference between the repeated measurement results (and thus, obviously, also from the true value). However, if a large number of repeated measurements are made then the mean value will have little influence from the random effects (situation 2 on the scheme). So, the influence of random effects can be decreased by increasing the number of repetitions. Systematic effects cause deviation of all measurements in the series into the same direction by the same magnitude. [4]It is more correct to say „by a predictable magnitude“. This means that the magnitude is not necessarily always the same – it can vary, e.g. as the magnitude of the measurand value varies – but it can be predicted, i.e. it is not random. Increasing the number of repetitions does not enable decreasing their influence (situation 3 on the scheme).
In principle it is desirable to determine the magnitude and direction of the systematic effects and correct the measurement results for the systematic effects. However, it can often be so difficult and work-intensive, that it becomes impractical. Therefore in many cases, rather than accurately determining the systematic effects and correcting for them their possible magnitudes is estimated and are taken into account as uncertainty sources. In lectures 5.4 and 6 random and systematic effects are treated more comprehensively.
There are in general four main sources of uncertainty in volumetric measurements, i.e. measurements by pipettes, burettes, measuring cylinders and volumetric flasks:
- Uncertainty due to the non-ideal repeatability of measurement (often called repeatability uncertainty). In the case of pipetting this means that however carefully we try to fill and empty the pipette, we will nevertheless every time get a slightly different volume. This is sometimes referred to as the “human effect” or the “human factor”, but in fact, if a machine would do the pipetting then there would also be difference between the volumes (although probably smaller). Repeatability is a typical random effect and contributes to uncertainty with glass pipettes as well as with automatic pipettes. Its influence on the measurement result can be decreased by making repeated measurements but it can never be entirely eliminated.
- Uncertainty due to calibration of the volumetric equipment (often called calibration uncertainty). In the case of volumetric glassware this is the uncertainty in the positions of the marks on the volumetric glassware. In the case of automatic pipettes this uncertainty is caused by the systematically too high or too low displacement of the piston inside the pipette. In the case of a given pipette it is a typical systematic uncertainty source. This uncertainty source can be significantly reduced by recalibrating the pipette in the laboratory by the person who actually works with it. Accurate weighing of water at controlled temperature is the basis of calibration of volumetric instruments and also the way how usually the repeatability uncertainties of different volumetric instruments are found.
- Uncertainty due to the temperature effect (often called as temperature uncertainty). All volumetric ware is usually calibrated at 20 °C and volumes usually refer to volumes at 20 °C. The density of the liquid changes (almost always decreases) with temperature. If pipetting is done at a higher temperature than 20 °C then there amount of liquid (in terms of mass or number of molecules) pipetted is smaller than if it were done at 20 °C. Consequently, the volume of that amount of liquid at 20 °C is also smaller than if the pipetting were done at 20 °C. In the case of volumetric glassware temperature affects the dimensions of the volumetric ware (its volume increases with temperature). The effect of liquid density change is ca 10 times stronger. Therefore the volume change of volumetric glassware is almost always neglected. In the case of automatic pipettes the effect of temperature is more complex. If the air inside the pipette warms then the delivered liquid volume can change to some extent. If the temperature of the laboratory and, importantly, temperature of the pipetted liquid, is constant during repeated measurements then the temperature effect is a systematic effect.
- Application-specific uncertainty sources. These are not caused by the volumetric equipment but by the liquid that is handled or by the system that is investigated. Some examples:
1. If a foaming solution is pipetted, measured by a volumetric flask or a measuring cylinder then it is not clear where exactly the solution “ends”, i.e., there is no well-defined meniscus. This will cause an additional uncertainty. Depending on situation this effect can be random or systematic or include both random and systematic part.
2. If titration is carried out using visual indicator then the end-point of titration, i.e. the moment when the indicator changes color is assumed to match the equivalence point (the stoichiometry point). However, depending on the titration reaction and on the actual analyte that is titrated, the end-point may come earlier or later than the equivalence point. In the case of the given titration this will be a systematic effect. This effect can be minimized by some other means of end-point detection, e.g. potentiometric titration. [5]In fact, even if the end-point is determined potentiometrically, it can still have some systematic deviation from the equivalence point. However, this effect is usually so small that it can be neglected.
There are some other uncertainty sources that usually turn out to be less important, because they can be minimized or eliminated by correct working practices (however, they can be important if these correctly practices are not applied). The remaining effects will usually influence the repeatability of pipetting or its calibration uncertainty and can be taken into account within those uncertainty sources.
- If the pipette is not kept vertically (both glass and automatic pipettes), waiting is not long enough after the end of drainage of solution (glass pipette) then the pipetted volume will be lower than the one obtained with correct pipetting. No waiting is needed in the case of automatic pipettes because no liquid film remains (and must not remain) on pipette to inner walls.
- When using a glass pipette then there is always some possibility that small residues of the previous solution are still in the pipette. It is therefore a good idea to rinse the pipette before pipetting (e.g. two times) with the solution that will be pipetted (and discarding the rinse solution it into waste, not into the vessel from where the solution is taken). In the case of automatic pipettes it is a good idea to use a new tip every time e new solution is pipetted. In that case such contamination is usually negligible. Also, when pipetting the same solution numerous times with the same pipetteit is a good idea to monitor it for the absence of droplets on the inner walls and replace the tip when the droplets appear.
- If the walls of a glass pipette are not clean then droplets may remain on the walls after the pipetted solution has been drained. This leads to a different volume from the case when no droplets are left on pipette walls after draining the solution. The obvious thing to do is to clean the pipette.
- If the pipetted liquid is very different from water (e.g. some highly viscous liquid, such as vegetable oil) then the pipetted volume may be systematically different from the nominal volume of the pipette. This effect exists both with glass pipettes and with automatic pipettes. In such a case the pipette should either be recalibrated using the liquid under question or weighing should be used instead of volumetry [6]In the case of automatic pipettes also reverese pipetting instead of the more common forward pipetting can be used to decrease the uncertainty when pipetting viscous liquids. .
In section 4 the uncertainty sources of pipetting (the same pipetting experiment that was performed in the video) will be quantified and combined into the measurement uncertainty estimate of pipetted volume. Sections 4.1 to 4.5 present the uncertainty calculation using a factory-calibrated pipette. Section 4.6 presents an example of measurement uncertainty calculation of pipetted volume using a self-calibrated pipette. In section 5 an overview of the majority of uncertainty sources that are encountered in chemical analysis will be given.
***
[1] This second video explains how to pipet with an automatic pipette if accurate volume is desired. In many routine, high-volume applications (e.g. in biochemistry), however, speed is more impoirtant than accuracy and in such cases some steps shown here, most importantly, rinsing, can be omitted. Also, in some cases there is a very limited volume available of the solution that is pipetted – in such case also rinsing is not possible. On the other hand, if still higher accuracy is desired then the so-called reverse pipetting technique can be used. Reverse pipetting is more accurate than the commonly used forward pipetting, which is the technique demonstrated and explained in this video.
[2] These sources also cause the existence of error and could therefore also be called error sources.
[3] It is in principle not wrong to call them random and systematic sources of uncertainty, but this is not usually done. This is largely because, as we will see in a coming lecture, the concept of measurement uncertainty stresses that random and systematic effects should be treated the same way.
[4] It is more correct to say „by a predictable magnitude“. This means that the magnitude is not necessarily always the same – it can vary, e.g. as the magnitude of the measurand value varies – but it can be predicted, i.e. it is not random.
[5] In fact, even if the end-point is determined potentiometrically, it can still have some systematic deviation from the equivalence point. However, this effect is usually so small that it can be neglected.
[6] In the case of automatic pipettes also reverese pipetting instead of the more common forward pipetting can be used to decrease the uncertainty when pipetting viscous liquids.


