1. The concept of measurement uncertainty (MU)

Brief summary: This section introduces the concepts of measurand, true value, measured value, error, measurement uncertainty and probability.

The concept of measurement uncertainty
http://www.uttv.ee/naita?id=17583 

https://www.youtube.com/watch?v=BogGbA0hC3k

Measurement is a process of experimentally obtaining the value of a quantity. The quantity that we intend to measure is called measurand. In chemistry the measurand is usually the content (concentration) of some chemical entity (molecule, element, ion, etc) in some object. The chemical entity that is intended be determined is called analyte. Measurands in chemistry can be, for example, lead concentration in a water sample, content of pesticide thiabendazole in an orange or fat content in a bottle of milk. In the preceding example lead (element), ascorbic acid (molecule) and fat (group of different molecules) are the analytes. Water, orange and milk are analysis objects (or samples taken from analysis objects).

In principle, the aim of a measurement is to obtain the true value of the measurand. Every effort is made to optimize the measurement procedure (in chemistry chemical analysis procedure or analytical procedure [1]) in such a way that the measured value is as close as possible to the true value. However, our measurement result will be just an estimate of the true value and the actual true value will (almost) always remain unknown to us. Therefore, we cannot know exactly how near our measured value is to the true value – our estimate always has some uncertainty associated with it.

The difference between the measured value and the true value is called error. Error can have either positive or negative sign. Error can be regarded as being composed of two parts – random error and systematic error – which will be dealt with in more detail in coming lectures. Like the true value, also the error is not known to us. Therefore it cannot be used in practice for characterizing the quality of our measurement result – its agreement with the true value.

The quality of the measurement result, its accuracy, is characterized by measurement uncertainty (or simply uncertainty), which defines an interval around the measured value C_MEASURED, where the true value C_TRUE lies with some probability. The measurement uncertainty U itself is the half-width of that interval and is always non-negative. [2] The following scheme (similar to the one in the lecture) illustrates this:

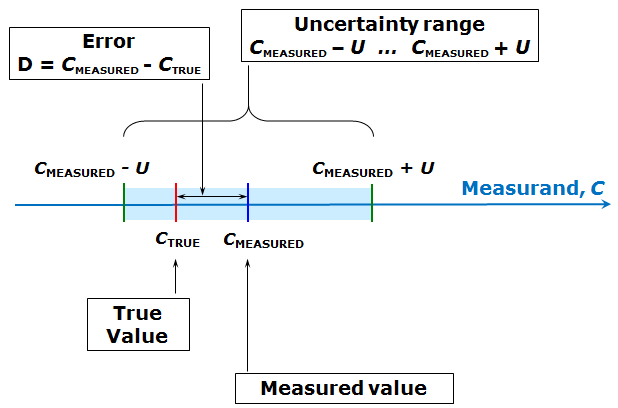
Scheme 1.1. Interrelations between the concepts true value, measured value, error and uncertainty.

Measurement uncertainty is always associated with some probability – as will be seen in the next lectures, it is usually not possible to define the uncertainty interval in such a way that the true value lies within it with 100% probability.

Measurement uncertainty, as expressed here, is in some context also called the absolute measurement uncertainty. This means that the measurement uncertainty is expressed in the same units as the measurand. As will be seen in subsequent lectures, it is sometimes more useful to express measurement uncertainty as relative measurement uncertainty, which is the ratio of the absolute uncertainty U_abs and the measured value y:

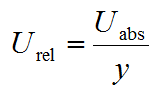(1.1)

Relative uncertainty is a unitless quantity, which sometimes is also expressed as per cent.

Measurement uncertainty is different from error in that it does not express a difference between two values and it does not have a sign. Therefore it cannot be used for correcting the measurement result and cannot be regarded as an estimate of the error because the error has a sign. Instead measurement uncertainty can be regarded as our estimate, what is the highest probable absolute difference between the measured value and the true value. With high probability the difference between the measured value and the true value is in fact lower than the measurement uncertainty. However, there is a low probability that this difference can be higher than the measurement uncertainty.

Both the true value and error (random and systematic) are abstract concepts. Their exact values cannot be determined. However, these concepts are nevertheless useful, because their estimates can be determined and are highly useful. In fact, as said above, our measured value is an estimate of the true value.

***

[1] Analytical chemists mostly use the term „analytical method“. In this course we use the term „procedure“ instead of „method“, as this usage is supported by the VIM.

[2] Here and in the lecture the capital U  is used to denote a generic uncertainty estimate. The symbol U  is picked on purpose, because expanded uncertainty (generally denoted by capital U ) fits very well with the usage of uncertainty in this section. However, it is not explicitly called expanded uncertainty here, as this term will be introduced in later lectures.