B. Standard substance (KIO3, see the picture) solution was prepared by weighing 0.21500 g of KIO3 into the 100 ml volumetric flask (see the picture) in the laboratory, which temperature didn’t differ from 20°C more than ±3°C. Uncertainty of filling the flask is not higher than ±1 drop (the volume of the drop is approximately 0.03 ml). The repeatability standard deviation of the balance used (with 5 decimal places) was 0.00021 g. The uncertainty due to calibration, drift and linearity of the balance can be considered insignificant. What is the concentration of the solution (unit g/l) and its combined standard uncertainty? Result and uncertainty must be presented with four decimal places and rounding must be done for the last digit.
Uncertainty components of
c(KIO
3) are: purity of the KIO
3 (
upurity), mass of the KIO
3 (
umass) and volume of the solution (
uvolume). Mathematical model:
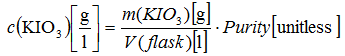
Actual purity is assumed to be exactly between maximum and minimum purity with the rectangular distribution. Uncertainty of the mass has two main components: repeatability and rounding of the digital reading. Uncertainty of the solution volume (uvolume) has three main uncertainty sources: calibration of the flask, filling of the flask and temperature changes.
[accordion][acctitle]Clue 3[/acctitle]The flask was not calibrated in the laboratory, so we have to use data given by the manufacturer. As it is seen from the picture, it is ±0.1 ml and the calibration was done at 20°C. Experiment was made at the temperature (20 ± 3) °C and uncertainty caused by the temperature changes is calculated according to eq 
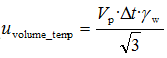
where γW=2.1·10-4 ·1/0C.[/accordion]
All contributing uncertainties should be expressed in the same units. In case of model that includes only multiplications and divisions is the correct way is to calculate the relative (unitless) standard uncertainties and then to combine those. Then you should multiply the relative uncertainty with the value of the result and you get the combined standard uncertainty with the same unit as the result.
