
Estimation of measurement uncertainty in chemical analysis
9.5. Step 5 – Standard uncertainties of the input quantities
Standard uncertainties of the input quantities
http://www.uttv.ee/naita?id=17641
https://www.youtube.com/watch?v=ZIEhfCoNyxU
Finding standard uncertainties of the input quantities
The standard uncertainty of Asample is found from the following three uncertainty components:
(1) The uncertainty due to the repeatability of photometric measurement:
u (Asample, rep) = 0.0010 AU (9.2)
This uncertainty includes the repeatability of the instrument, repeatability of positioning the cell in the instrument and possible disturbances, such as a random dust particle on the optical windows of the cell.
(2) The uncertainty due to the possible drift of the spectrophotometer parameters:
u (Asample, drift) = 0.0012 AU (9.3)
(3) The uncertainty due to the possible interfering effects:
u (Asample, chem) = 0.0030 AU (9.4)
These can be due to some other compound (interferent) absorbing (or scattering) light at the same wavelength that is used for measurement (leading to increase of the absorbance value) or due to some disturbance in forming the photometric complex (leading to decrease of the absorbance value).
As a result:
| (9.5) |
We see that uncertainty due to possible interference dominates the uncertainty budget of sample absorbance. Although in this example accounting for possible interferences is easy, in reality quantitative evaluation of uncertainty due to possible interference is difficult. Some practical advice on this is given below in the section “Evaluating uncertainty due to possible interference”.
The standard uncertainties of the slope b1 and intercept b0 are in this example found as standard deviations of the respective regression coefficients (see the XLS files in section 9.7). This is an approximate way of taking into account the uncertainty due to calibration graph and linear regression analysis, because it (1) neglects the systematic effects affecting all the points on the regression line (e.g. weighing and purity of the standard substance) and (2) neglects the negative correlation between b1 and b0 (which always exists). The first of these effects leads to some underestimation of uncertainty and the second one leads to some overestimation of uncertainty. So, this approach should only be used if it is not expected that calibration graph and linear regression analysis will be among the main contributors to uncertainty. This usually holds if the standard substance has high purity, can be weighed accurately and if the scatter of data points around calibration graph is not high. [1]
The u(fd) is found on an assumption that the relative combined standard uncertainty of all involved volumetric operations is not higher than 0.5%. If volumetric operations are carried out carefully then this is a safe assumption under usual laboratory conditions. Considering that the value of fd is 1.25 (unitless) we get the following:
u (fd) = 1.25 · 0.5% / 100% = 0.0065 (unitless) (9.6)
The uncertainty of ΔCdc accounts for possible decomposition of the photometric complex and possible contamination of the sample. The word “possible” is stressed here: it is well possible that actually there is neither decomposition of the photometric complex nor contamination of the sample. However, in order to rigorously establish this, extensive research would be needed. Therefore in this example we use an estimate based on experience from our laboratory:
u (ΔCdc) =0.004 mg/l (9.7)
The standard uncertainties of the input quantities are summarized in table:
Table 9.1. Standard uncertainties of the input quantities in the measurement model (eq 9.1).
| Quantity | Value | u | Unit |
| Asample | 0.1860 | 0.0034 | AU |
| b0 | 0.0171 | 0.0025 | AU |
| b1 | 0.9808 | 0.0046 | AU×l/mg |
| fd | 1.2500 | 0.0063 | – |
| ΔCdc | 0.0000 | 0.0040 | mg/l |
Evaluating uncertainty due to possible interference
There is no universally applicable way of evaluating uncertainty due to possible interference. The most rigorous approach is separately determining the content of the interfering compounds in the sample and correcting the result (then of course the uncertainty of correction has to be evaluated but that is easier). However, in most cases running separate analysis for determining the (possible) interferents is far too labor-intensive for being practical. The matter is further complicated by the limited information that is usually available about the interferents: it is usually not known what the compounds that cause interference are. For this reason, if the interference is not too strong then the usual approach is to try to take it into account by increasing the measurement uncertainty [2].
The following are two examples how the uncertainty due to (possible) interfering compounds can be taken into account in measurement uncertainty estimation.
1. Obtaining and using interference information from spectra. The following scheme presents a situation where interference is clearly present and can be seen from the appearance of the spectra:
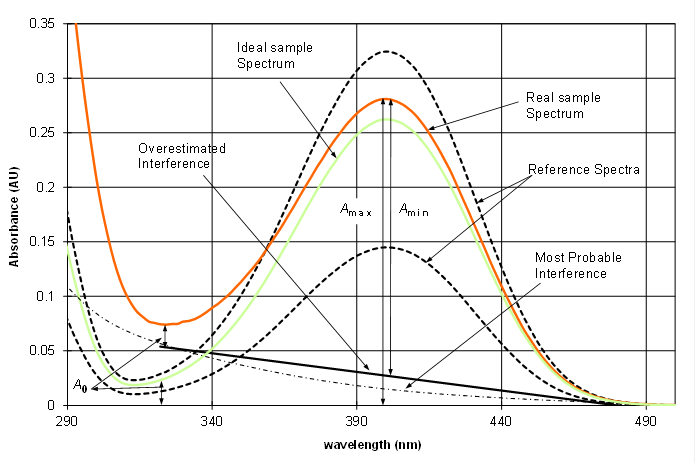
Scheme 9.2. UV-Vis absorbance spectra of calibration solutions (dotted lines), sample solution with interference (red line) and ideal (theoretical) sample solution where no interference is present.
The dotted spectra are the analyte spectra in the calibration solutions (reference spectra) where the correct shape of the spectrum can be seen. The green line corresponds to the “theoretical” – i.e. devoid of any interference – spectrum of the sample solution. Red line corresponds to the actual (experimental) spectrum of the sample solution. The most probable spectrum of the interferent [3] is presented by the dash-dot line. Its shape suggests that it is a sum of a large number of different organic compounds – quite common situation.
The absorbance at 400 nm (wavelength of the absorbance maximum) is the analytical signal. It is obvious from the scheme that when simply measured from the “red” spectrum (Amax) it leads to overestimated absorbance. Using the “green” spectrum or the spectrum of the interferent is impossible, because neither of the two is available.
In this situation one can try to estimate the probable maximum and minimum absorbance values (A) of the analyte, corresponding to the probable minimum and maximum, respectively, interference. A good estimate of the maximum A is Amax (it corresponds to the not very likely situation that there is no interference at 400 nm and the whole A is due to analyte). For estimating the minimum A we assume linear relation between the interfering effect and wavelength as presented by the solid line tagged “Overestimated interference”. It is overestimated in the sense that the absorbance at 400 nm is higher than the probable interference. This line is defined as follows. It is fixed to zero at 480 nm (it is clear that there is no interference at that wavelength). At wavelength 322 nm the line is fixed in such a way that the A difference from the spectrum with interference is the same as the difference of the (estimated) spectrum without interference from zero at 322 nm (both denoted as A0 on scheme 9.2).
From the values of Amin and Amax the corrected absorbance (to be used for calculation of the result), as well as its uncertainty component due to interference can be found as follows:
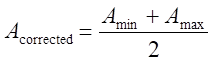 |
(9.8) |
 |
(9.9) |
This approach is approximate but its advantage is that it can be used in the case of unknown interferents.
2. Using interference data from previous studies. If validation included interference studies and the interference was quantitatively described then these data can be used for correcting the result and obtaining the uncertainty estimate due to possible interference. As an example, let us look at selectivity data in the standard method ISO 7150:1984 of spectrophotometric ammonium nitrogen determination. Table 9.2. presents the data about the influence of selected interferents.
Table 9.2. Influence of selected interferents on ammonium nitrogen determination according to ISO 7150:1984 (data from ISO 7150:1984).
| Interferent, B | CB (mg/l) | Influence of B on CN (mg/l) at the following CN (mg/l) values: |
||
| 0 | 0.2 | 0.5 | ||
| Cl¯ | 1000 | +0.002 | +0.013 | +0.033 |
| CN¯ | 5 | +0.002 | +0.019 | +0.016 |
| PO43¯ | 100 | 0 | -0.001 | -0.015 |
| Ethanolamine | 1 | +0.16 | +0.11 | — |
Let us take interference from chloride as an example. Suppose we know that our sample may contain chloride and its content is certainly below 800 mg/l and we have found CN in the sample around 0.2. In that case the maximum interference would be +0.013 x 800 / 1000 = 0.0104 mg/l. If we do not know the amount of chloride in the sample and if determining it separately would be impractical then we can assume that the chloride content is (400 ± 400) mg/l. This uncertainty range embraces the whole concentration range from 0 to 800 mg/l. The interference corresponding to this chloride content would be +0.0052 mg/l and it can be used for correcting the obtained CN value (by subtracting it from CN). Its standard uncertainty, if rectangular distribution is assumed is 0.0052 / sqrt(3) = 0.0030 mg/l. this uncertainty should be additionally included in the uncertainty budget.
3. Using interference data via model equation. Sometimes the measurement model can be used directly for taking interference into account. An example of this situation can be found in Self-test 9 C.
***
[1] The same example solved with full rigor is available from https://akki.ut.ee/GUM_examples/. Please look at the example “Ammonium by Photometry” with elaboration level “High (uncertainty estimated at full rigor, suitable for experts)”. Comparison of the obtained combined uncertainties: 0.00686 mg/l obtained here (section 9.7) and 0.0065 mg/l obtained with full rigor shows that this approach is acceptable, especially since it leads rather to uncertainty overestimation than underestimation.
[2] If the interference is really strong for a specific matrix then analysis procedure should be modified and revalidated.
[3] Approximately this shape of the spectrum is usually observed, if a large number of different compounds are present, each one at very low level. Furthermore, the way the analyte spectrum in the sample is distorted implies exactly this shape of interferent spectrum.


