7. Precision, trueness, accuracy

Brief summary: Interrelations between the different error types (random, systematic, total), their corresponding performance characteristics (precision, trueness, accuracy) and the parameters for quantitatively expressing these performance parameters (standard deviation, bias, measurement uncertainty) are explained in this section.

Interrelation between the concepts of precision, trueness, accuracy and measurement uncertainty
http://www.uttv.ee/naita?id=17824

https://www.youtube.com/watch?v=NdDK03f0wew

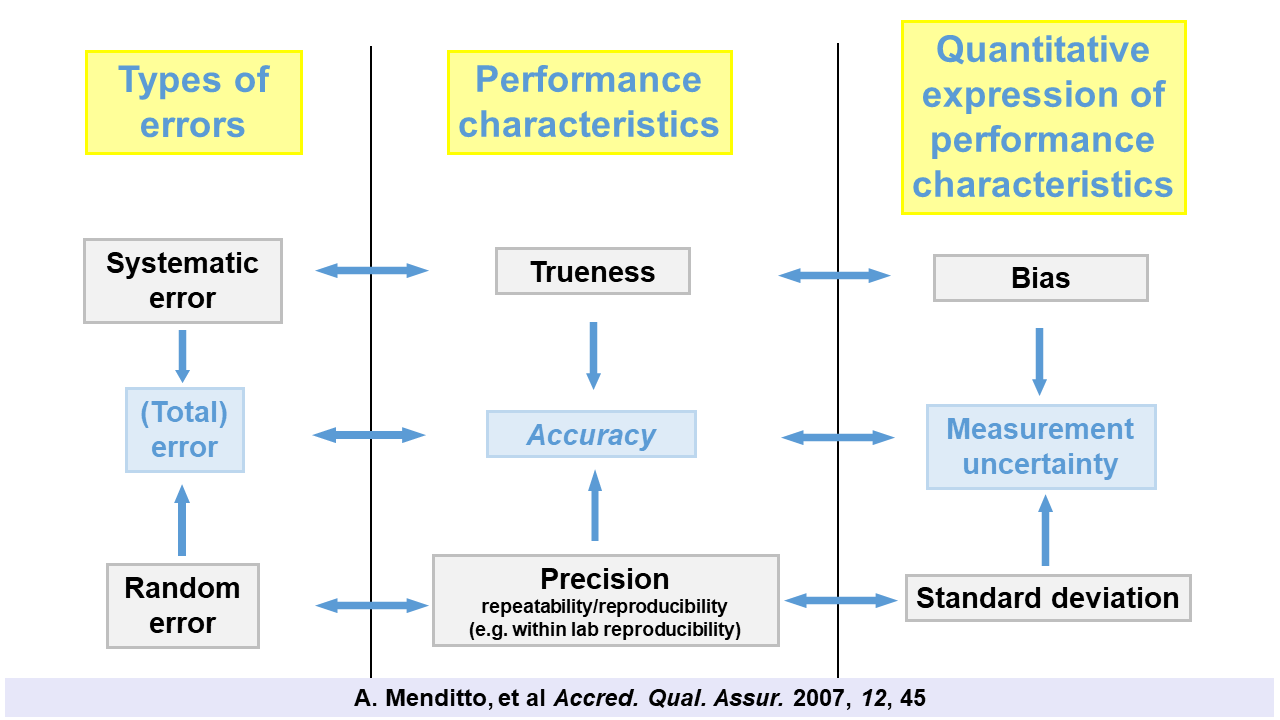
Scheme 7.1. Interrelations between the different error types, the performance characteristics used to estimate them and the ways of expressing the estimates quantitatively. This type of scheme was originally published in article A. Menditto, et al Accred. Qual. Assur. 2007, 12, 45.

The difference between the measured value and the true value is called error or total error (see section 1). This error can be divided into two parts – random error (having different magnitude and sign in the case of repeated measurements) and systematic error (having the same or systematically changing magnitude and sign in the case of repeated measurements). As seen in section 1 errors cannot be known exactly. Therefore instead of errors themselves we operate with estimates of errors – the performance characteristics.

Thus, trueness is the estimate of the systematic error. For determining trueness we do not need to know the true value but we need to know a reference value. Reference value (differently from the true value) has uncertainty, but usually a small one. Different types of precision are estimates of the random error. For obtaining the “true” precision we would need to make an infinite number of repeated measurements. There are different types of precision, depending on the conditions under which precision is determined, e.g. repeatability (section 1) and intermediate precision (section 6). Accuracy embraces both trueness and precision and be considered as describing the total error.

These performance characteristics can be quantitatively expressed. Bias – difference between the measured value obtained from multiple repeated measurements with the same sample and the reference value – is the quantitative expression of trueness. Standard deviation – again obtained from multiple measurements with the same sample – is the quantitative expression of precision. These two can be combined into a measurement uncertainty estimate, which can be regarded as the quantitative expression of accuracy.