3.4. Standard deviation of the mean

Brief summary: Like the individual values, the mean value calculated from them is also a random quantity and for it also a standard deviation can be calculated. It is possible to calculate it from the standard deviation of the individual value. It is explained when to use the standard deviation of the individual value and when to use the standard deviation of the mean: whenever the individual result is used in further calculation the standard deviation of the individual result has to be used; whenever the mean value is used in further calculations, the standard deviation of the mean has to be used.

Standard deviation of the mean
http://www.uttv.ee/naita?id= 17580

https://www.youtube.com/watch?v=GLsHHIW1yjo

The standard deviation s (V ) calculated using the formula 3.3 is the standard deviation of an individual  pipetting result (value). When the mean value is calculated from a set of individual values which are randomly distributed then the mean value will also be a random quantity. As for any random quantity, it is also possible to calculate standard deviation for the mean s (V_m ). One possible way to do that would be carrying out numerous measurement series, find the mean for every series and then calculate the standard deviation of all the obtained mean values. This is, however, too work-intensive. However, there is a very much simpler approach for calculating s (V_m ), simply divide the s (V ) by square root of the number of repeated measurements made:

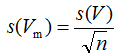(3.5)

So, for a set of repeated pipetting values we have in fact two standard deviations: standard deviation of the single value s (V ) and standard deviation of the mean s (V_m ). It is important to ask: when we use one and when another of them?

The general rule of thumb is the following: when the measured value reported or used in subsequent calculations is a single value then we use standard deviation of the single value; when it is the mean value then we use the standard deviation of the mean.

Let us illustrate this by two examples:

1. Pipetting. When we deliver a certain volume by a pipette then pipetting is a one-time operation: we cannot repeat the pipetting with the same liquid amount. So we use the standard deviation of single pipetting as pipetting repeatability uncertainty.
2. Weighing. When we weigh a certain amount of a material then we can weigh it repeatedly. So, if we need to minimize the influence of weighing repeatability in our measurement then we can weigh the material repeatedly and use in our calculations the mean mass. In this case the repeatability standard deviation of this mean mass is the standard deviation of the mean. If, on the other hand, it is not very important to have the lowest possible repeatability uncertainty of mass then we weigh only once and use the mass value from the single weighing and as its repeatability uncertainty we will use the standard deviation of a single value. [1]

In the case of single pipetting or single weighing the repeatability uncertainty of course cannot be estimated from this single operation. In these cases repeatability is determined separately and then used for the concrete measurements.

***
[1] As we will see later, modern balances are highly accurate instruments and uncertainty due to weighing is seldom among the important uncertainty sources. So, unless some disturbing effects interfere with weighing, it is usually not necessary to weigh materials with many repetitions.