
Estimation of measurement uncertainty in chemical analysis
3.2. Mean, standard deviation and standard uncertainty
Brief summary: the lecture explains calculation of mean (Vm) and standard deviation (s). Illustrates again the 68% probability of s. Explains how the standard uncertainty of repeatability u (V, REP) can be estimated as standard deviation of parallel measurement results. Stresses the importance of standard uncertainty as the key parameter in carrying out uncertainty calculations: uncertainties corresponding to different sources (not only to repeatability) and to different distribution functions are converted to standard uncertainties when uncertainty calculations are performed.
Mean, standard deviation and standard uncertainty
http://www.uttv.ee/naita?id=17554
https://www.youtube.com/watch?v=ND3iryaVQ68
One of the most common approaches for improving the reliability of measurements is making replicate measurements of the same quantity. In such a case very often the measurement result is presented as the mean value of the replicate measurements. In the case of pipetting n times with the same pipette volumes V1, V2, …, Vn are obtained and the mean value Vm is calculated as follows:
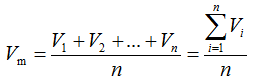 |
(3.2) |
As explained in section 3.1, the mean value calculated this way is an estimate of the true mean value (which could be obtained if it were possible to make an infinite number of measurements).
The scatter of values obtained from repeated measurements is characterized by standard deviation of pipetted volumes, which for the same case of pipetting is calculated as follows:
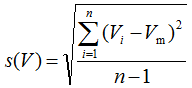 |
(3.3) |
The n – 1 in the denominator is often called number of degrees of freedom. We will see later that this is an important characteristic of a set or repeated measurements. The higher it is the more reliable mean and standard deviation can be from the set.
Two important interpretations of the standard deviation:
- If Vm and s (V ) have been found from a sufficiently large number of measurements (usually 10-15 is enough) then the probability of every next measurement (performed under the same conditions) falling within the range Vm ± s (V ) is roughly 68.3%.
- If we make a number of repeated measurements under the same conditions then the standard deviation of the obtained values characterized the uncertainty due to non-ideal repeatability (often called as repeatability standard uncertainty) of the measurement: u (V, REP) = s(V). Non-ideal repeatability is one of the uncertainty sources in all measurements. [1]
Standard deviation is the basis of defining standard uncertainty – uncertainty at standard deviation level, denoted by small u. Three important aspects of standard uncertainty are worth stressing here:
- Standard deviation can be calculated also for quantities that are not normally distributed. This enables to obtain for them standard uncertainty estimates.
- Furthermore, also uncertainty sources that are systematic by their nature and cannot be evaluated by repeating measurements can still be expressed numerically as standard uncertainty estimates.
- Converting different types of uncertainty estimates to standard uncertainty is very important, because as we will see in section 4, most of the calculations in uncertainty evaluation, especially combining the uncertainties corresponding to different uncertainty sources, are carried out using standard uncertainties.
Standard uncertainty of a quantity (in our case volume V) expressed in the units of that quantity is sometimes also called absolute standard uncertainty. Standard uncertainty of a quantity divided by the value of that quantity is called relative standard uncertainty, urel (similarly to eq 1.1). In the case of volume V:
| (3.4) |
[1] We will see later that standard deviation of measurements repeated under conditions that changer in predefined way (i.e. it is not repeatability) is also extremely useful in uncertainty calculation, as it enables taking a number of uncertainty sources into account simultaneously.


