
Estimation of measurement uncertainty in chemical analysis
10.3. Uncertainty component accounting for systematic effects
Estimating the uncertainty component due to possible bias
http://www.uttv.ee/naita?id=17910
https://www.youtube.com/watch?v=hLGZsW_o81o
The component u (bias) takes into account possible bias of the measurement procedure.
Reliably determining the bias of the procedure is not easy for the following reasons:
- If the random effects are strong then this needs a very large number of measurements. When a limited number of measurements are made then the bias estimate will always contain a contribution from random effects, which will make the bias estimate artificially higher. Even more so – the procedure can actually have no bias at all.
- Even with formally similar matrixes the bias can differ by magnitude and even by sign (e.g. when determining pesticides in different varieties of apples, determining drug residues in blood plasma from different patients, etc). This means that having determined the bias in one variety of apples this bias is not automatically applicable for another variety and we can speak about uncerteinty in applying the bias to another variety.
- Bias is always determined against a reference value, which also has an uncertainty.
This is why we speak about possible bias and the uncertainty component u (bias) quantifies our limited knowledge about bias.
Bias refers to difference between our measured value and a reference value. Therefore, for finding u (bias) we need a sample or a material with a reference value. In broad terms there are four different possibilities how the u (bias) can be determined:
|
Possibility of determining u (bias) |
Pros |
Cons |
| Analysing the sample with a reference analysis procedure | Bias can be determined very reliably, because the determined bias corresponds to the bias with exactly the same sample matrix as is in the real sample. | It is usually very difficult to find a suitable reference procedure. Therefore this possibility is not often used at routine labs. |
| Certified reference material (CRM) [1] | Bias can be determined quite reliably, because the reference values of CRM-s are generally quite reliable. | Availability of certified reference materials is limited and their matrixes are often better homogenised than in the case of real samples, leading to somewhat optimistic bias estimates. |
| Using samples of interlaboratory comparisons as reference samples | Is often usable at routine labs, because labs usually participate in interlaboratory comparisons with the procedures that they use in their everyday work. | The reference values are mostly derived from participant results and have therefore low reliability (high uncertainty). This leads to overestimated u (bias). |
| Using spiking studies | Can be done at the laboratory and can be done with the real samples, thereby exactly matching the matrix. | The main problem in bias determination by spiking is dispersing the analyte in the sample in the same way as the native analyte in the sample. In the case of inhomogenous matrixes this can be very difficult. |
In the case of all four possibilities it is critical to include also sample preparation in bias determination.
In the case of all four possibilities it is necessary to make an as large as possible number of replicate measurements in order to separate the bias from random effects as efficiently as possible. Bias generally changes from matrix to matrix and usually is different at different concentration levels. So, it is important to use several CRMs, several interlaboratory comparisons, etc.
The lower is the reliability of the reference value the higher is the u (bias) estimate.
The u (bias) component is found according to the following equation:
| (10.2) |
RMSbias is the average (root mean square) bias and is found as follows:
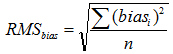 |
(10.3) |
Where n is the number of bias determinations carried out and each biasi is a result of an individual bias determination and is found as follows:
| (10.4) |
Where Clabi is a mean of the results of analyte determination in the reference sample (e.g. in the CRM) obtained by the laboratory and Crefi is the reference value of the reference sample. It is important that Clabi corresponds to a number of replicates.
u (Cref) is the average standard uncertainty of the reference values of the reference samples and is found as follows:
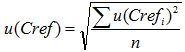 |
(10.5) |
Here u (Crefi) is the standard uncertainty of the i-th reference value. In the case of CRM analysis, spiking or analysis with a reference procedure the u (Crefi) can usually be reasonably found. However, in the case of interlaboratory comparisons where the consensus value of the participants is used as the reference value a reliable uncertainty of the reference value cannot be found. The best estimate in that case would be the standard deviation of the average value after elimination of outliers:
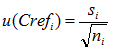 |
(10.6) |
Here si is the standard deviation of the participants in the i-th intercomparison after elimination of outlayers and ni is the number of participants (again after eliminating the outliers) in the i-th intercomparison.
In the special case if a number of bias determinations were carried out using one single CRM the equation 10.2 changes into the following form:
| (10.7) |
Where sbias is the standard deviation of the bias estimates obtained and n is the number of bias estimates obtained.
Depending on situation the u(bias) can be used as absolute or as relative value.
Finally, it is important to stress that the bias uncertainty component should be estimated separately for different matrixes and different concentration levels.
***
[1] In simplified terms certified reference material is a material, in which the content of the analyte (or analytes) is reliably known (the material has a certificate). If the certified reference material’s matrix is similar to real samples (i.e. it is not a pure compound or a solution but is e.g. milk powder, soil or blood plasma) then we call it certified matrix reference material.


