
Sotsiaalse Analüüsi Meetodite ja Metodoloogia õpibaas
Usaldusvahemik
Liina-Mai Tooding
Kadri Rootalu
2014
Usaldusvahemik (a,b) katab parameetri väärtuse populatsioonis (üldkogumis, kõigi vaadeldavate indiviidide seas) teatud läve ületava tõenäosusega (vt Tooding, 2007, ptk 4.1.2). Parameetriks võib olla keskmine (ka allpool olevates juhistes), dispersioon, osakaal, korrelatsioonikordaja, regressioonikordaja jne. Tõenäosuse läve nimetatakse usaldusnivooks ja see valitakse olenevalt tunnuse tähendusest ja tulemuse tähtsusest: tavapäraselt 95%, rangematel juhtudel 99%, aga miks mitte ka 90%. Usaldusvahemik leitakse nii, et ainult väikese tõenäosusega (eespool nimetatud juhtudel vastavalt kuni 5%, 1% ja 10%) võiks parameetri tegelik väärtus olla väljaspool usaldusvahemikku. Arve a ja b nimetatakse vastavalt alumiseks ja ülemiseks usalduspiiriks. Usalduspiire väljendatakse tunnuse ühikuis, kui tunnusel on mõõtühik.
Usaldusvahemik võiks olla ka ühepoolne, mil kas alumine või ülemine otspunkt jäetakse määramata. Sel juhul saame parameetri populatsiooni väärtuse jaoks vastavalt kas ainult ülemise või alumise tõkke.
Oluline on mõista, mis osutub usaldusvahemiku puhul juhuslikuks. Juhuslikud on juhusliku valimi alusel leitud usalduspiirid, mitte aga parameetri tõeline ehk tegelik väärtus (st parameetri väärtus populatsioonis), mis on kindel, kuigi meile tundmatu (vt nt siia). Tundmatuks see jääbki ja teame üksnes valimi põhjal saadud punkthinnangut (kui ei kasuta usaldusvahemikku) või vahemikhinnangut (kui kasutame usaldusvahemikku).
Millised plussid ja miinused on usaldusvahemikul võrreldes punkthinnangu ehk ühe konkreetse arvuga? Näiteks keskmise vahemikhinnang osutab tunnuse skaala osale, millel paikneb populatsiooni keskmine, lisades juurde ka sellise osutuse tõepärasuse. Miinuseks on punkthinnanguga võrreldes suurem ebamäärasus – kõneleme mitte ühest arvust, vaid teatavast pluss-miinusosast valimikeskmise ümber. Allpool toodud näites leitakse, et Euroopa sotsiaaluuringu järgi oli Eesti andmeil keskmine enesehinnanguline positsioon ühiskonnas 5,3 (väljendatuna skaalal 0–10). Keskmise usaldusvahemikuks osutub usaldusnivool 95% lõik 5,23–5,37 (täpsusega on meil natuke üle pingutatud). Kui mõttemänguna võtaksime korduvalt, sõltumatult ja ühetaoliselt valimeid Eesti populatsioonist, siis võib kindel olla, et vähemalt 95 valimi puhul sajast katab valimi alusel (usaldusnivool 95%) arvutatav usaldusvahemik keskmise tegeliku väärtuse (st keskmise väärtuse populatsioonis).
Intuitiivselt on arusaadav, et kitsam usaldusvahemik oleks tulemusena soovitavam kui lai. Millest oleneb usaldusvahemiku laius? Üldiselt võib öelda, et kaalukeeleks on kolm suurust: valimimaht, tunnuse hajuvusaste ja usaldusnivoo. Mida kõrgem usaldusnivoo, seda laiem usaldusvahemik (kui valimimaht ja hajuvus on sama). Mida suurema hajuvusega on tunnus, seda laiema usaldusvahemiku saame (sama valimimahu ja usaldusnivoo korral). Mida väiksem on valim, seda laiem on usaldusvahemik (sama hajuvusaste ja usaldusnivoo korral). Kahte head – konkreetsust ehk kitsast usaldusvahemikku ja kõrget usaldusväärsust – ei ole võimalik korraga saavutada, iseäranis kui andmeid on napilt.
Usaldusvahemik leitakse klassikalise skeemi kohaselt iga konkreetse parameetri jaoks detailides erisuguse reegli kohaselt, toetudes ühelt poolt tunnuse jaotuse iseloomule ja teiselt poolt vastavale teoreetilisele tulemusele. Üldskeem on sama: parameetri punkthinnang pluss-miinus tunnuse hajuvusest, valimimahust ja usaldusnivoost sõltuv osa. Tuntakse ka usaldusvahemiku hindamise avaramaid meetodeid, mis ei nõua tunnuse jaotuse kohta rangeid eeldusi.
Usaldusvahemike kõrvutamine ühe ja sama usaldusnivoo korral ühe ja sama tunnuse jaoks eri gruppides võimaldab teha järeldusi gruppide võrdlemiseks selle parameetri (nt keskmise) alusel, mille kohta on usaldusvahemik leitud. Usaldusvahemike mittekattumine (või kattumine vähesel määral) kõneleb gruppide erinevusest vaadeldava parameetri seisukohalt, tugev kattumine ühetaolisusest. Kui meie näites vaadelda, kuidas hindasid oma positsiooni ühiskonnas naised ja mehed, siis saame naiste jaoks keskmiseks 5,26±0,09 ja meeste jaoks 5,35±0,11. Nende kahe vahemiku — 5,17…5,35 ja 5,24…5,46 — kattuvuse ala on 5,24 (meeste alumine usalduspiir) kuni 5,35 (naiste ülemine usalduspiir), mis sisaldab ka mõlemad keskmised (tõsi küll, teise neist piiripealselt). Sellise suure kattuvuse korral ei ole statistiliselt põhjust kinnitada naiste ja meeste erisugust positsiooni ühiskonnas.
Andmestik ess12eesti.sav
Usalduspiiride tellimiseks paketis SPSS saab kasutada kirjeldava statistika menüüd (joonis 1).
Analyze – Descriptive Statistics – Explore
Näites soovime leida usalduspiirid tunnusele „Koht ühiskonnas“.
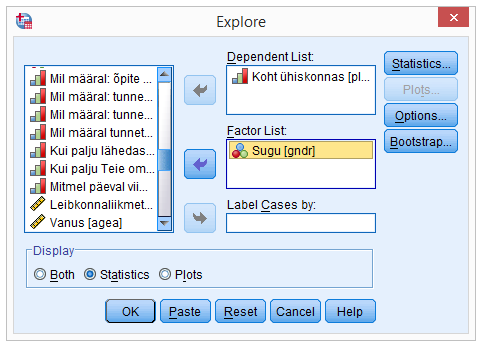
Avanenud tellimisaknas tuleks lahtrisse „Dependent List“ saata see arvuline tunnus, mille keskmise usalduspiire soovime leida (joonis 2). Vaadeldaval juhul on selleks „Koht ühiskonnas“.
Akende all osas „Display“ on võimalik määrata, kas soovime näha väljundis tabeleid („Statistics“), jooniseid („Plots“) või mõlemat („Both“). Kuna soovime tulemusi tabelis, siis sobib praegu variant „Statistics“, aga tulemuse saaksime ka variandiga „Both“.
Usaldusvahemike tellimiseks tuleb parempoolsest menüüst „Statistics“ märkida ära usaldusvahemiku laius, milleks praeguses näites on 95% (joonis 3).
Tulemused esitatakse kahe tabelina, millest huvipakkuvam on teine (pealkirjaga „Descriptives“).
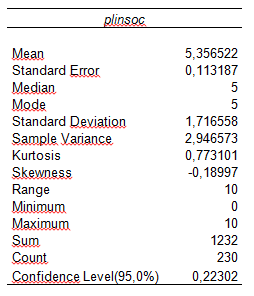
Tabel 1. Kirjeldav statistika ja usalduspiirid
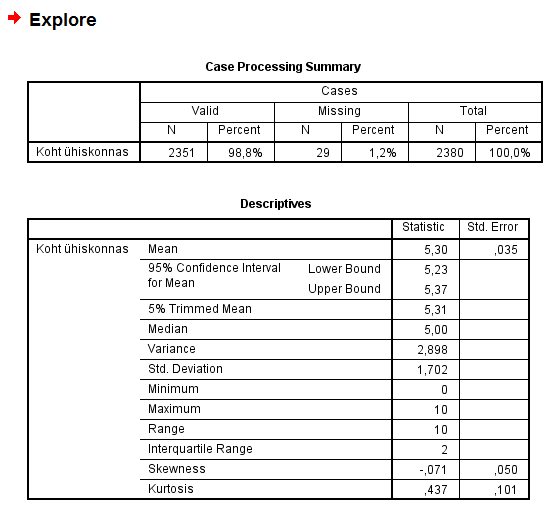
Tabelist „Descriptives“ selgub, et keskmine hinnang enda kohale ühiskonnas on 5,3 punkti. 95% usalduspiirid on vastavalt 5,23 (alumine) ja 5,37 (ülemine).
Keskmise usalduspiire saab leida ka mitmele grupile võrdlevalt. Näiteks soovime leida usalduspiirid tunnusele „Koht ühiskonnas“ meestele ja naistele eraldi. Tellimisaknas (joonis 4) tuleb selleks tunnus „Sugu“ saata lahtrisse „Factor List“.
Tabel 2. Usalduspiirid vastajate soo kaupa
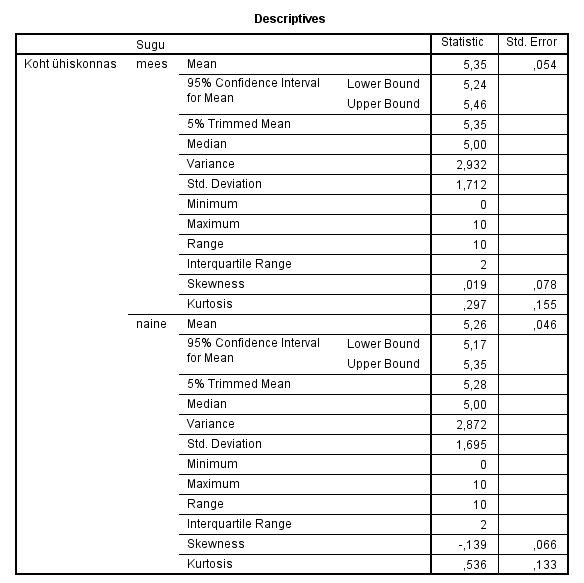
Tabelist 2 selgub, et meeste ja naiste keskmiste hinnangute 95% usaldusvahemikud kattuvad. Meeste puhul on selleks 5,24…5,46 punkti, naistel 5,17…5,35 punkti. Seega on võimalik, et üldkogumi keskmise hinnangud asuvad mõlema grupi puhul samas punktis.
Usaldusvahemike võrdlemiseks on võimalik kasutada ka jooniseid (SPSSis nimetusega „Error Bar“). Selleks tuleb jooniste tellimise menüüst („Graphs“) valida joonise tüübiks „Error Bar“ (vt joonis 5).
Avanevas tellimisaknas (joonis 6) tuleb valida lihtne joonis („Simple“) ning alumises valikumenüüs jätta variant „Summaries for groups of cases“. Vajutada nupule „Define“.
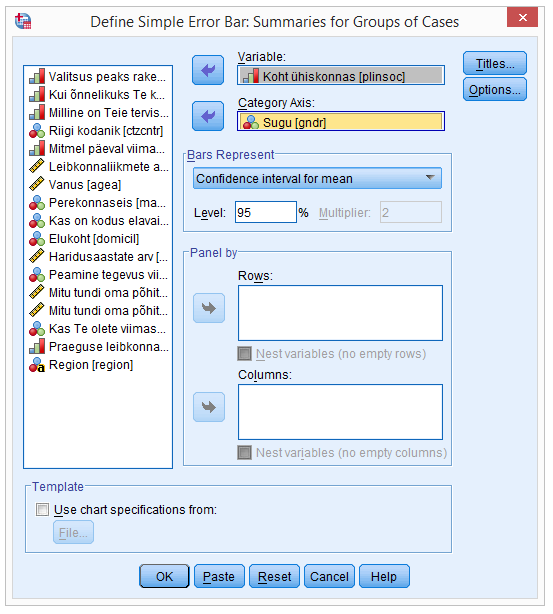
Avanev tellimisaken võimaldab valida arvulise tunnuse keskmise usalduspiiride arvutamiseks (lahter „Variable“). Vaadeldaval juhul on selleks „Koht ühiskonnas“ (vt joonis 7). X-teljele („Category Axis“) tuleb panna grupeeriv tunnus, milleks praegu on vastaja sugu.
Alajaotus „Bars Represent“ võimaldab valida usaldusvahemiku laiuse (95%).
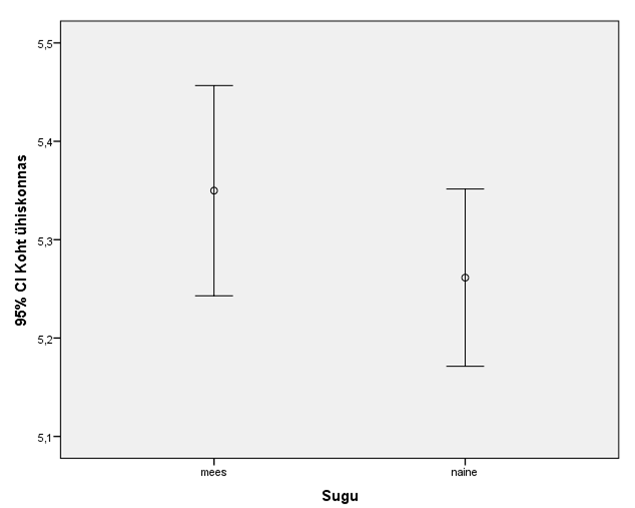
Tulemus on esitatud joonisel 8. Sellest võib näha, et meeste ja naiste usaldusvahemikud kattuvad. Seega võib arvata, et mehed ja naised ei hinda enda kohta ühiskonnas märkimisväärselt erinevaks.
Avage andmestik ess12eestiexcel-1.xls
Usaldusvahemiku leidmine Excelis on võimalik kirjeldava statistika mooduli abil (vt joonis 1)
Vajadusel vaadake: andmeanalüüsi mooduli aktiveerimine
Data Analysis – Descriptive Statistics
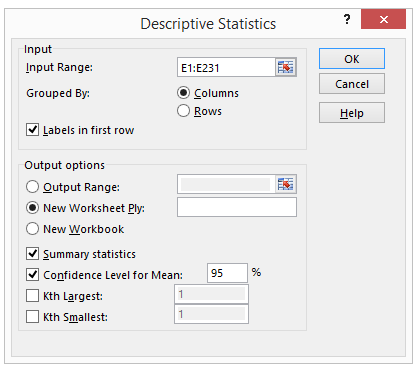
Tellimisaknas (joonis 2) tuleb määrata tunnus(t)e asukoht aadressina töölehel („Input Range“), tunnuste paigutus (veergudes või ridades, alajaotusest „Grouped By“), tunnuse nimede olemasolu esimesel valitud real („Labels in first row“).
Kirjeldava statistika tellimiseks märkida ära „Summary statistics“ ning usaldusvahemike tellimiseks „Confidence Level for Mean“ (joonis 2). Näites soovime 95% usaldusvahemike leidmist.
Saadavas tulemuste tabelis (tabel 1) antakse pool usaldusvahemiku laiusest viimasel real (nimetusega „Confidence Level“ (95%)). Usalduspiiride leidmiseks tuleb vahemik vastavalt liita (ülemine usalduspiir) või lahutada (alumine usalduspiir) keskmisest (5,36).
Tabel 1. Kirjeldav statistika ja usaldusvahemiku laius.
Märksõnad: usaldusnivoo, usaldusvahemik, alumine usalduspiir, ülemine usalduspiir.


