1. Põhimõisted

1.1 Elektromagnetlaine lähendused

Valguse elektromagnetlaineteooria opereerib vektorsuurustega . Mingi konkreetse probleemi lahendamiseks on meil vaja lahendada osatuletistega diferentsiaalvõrrandite süsteem. Lahendamiseks on vaja teada nii ainevõrrandeid (st seoseid  ja ) kui ka ääretingimusi. Ka juba suhteliselt lihtsate probleemide lahendamisel tekivad suured matemaatilised raskused. 
Laineoptika lähendus vaatleb valgust skalaarse ristlainena, mida iseloomustab amplituud ja faas. Enamik interferentsi ja difraktsiooni probleeme lahenduvad laineoptika lähenduses piisava täpsusega, nt valguse difrageerumisel aval ilmnevad mõneprotsendilised erinevused elektromagnetlaineteooria arvutustest alles juhul, kui ava mõõtmed on väiksemad kui viiekordne lainepikkus. 
Kui on vaja leida kujutise tekkimist läätses, osutub ka laineoptika lähendus tarbetult keerukaks. 
Geomeetrilise optika (kiirteoptika) lähenduses loetakse lainepikkust  tühiselt väikeseks; valgust iseloomustatakse energia levikusuunaga – kiirega. 
Edaspidi loeme keskkonna, kus levib valgus, isotroopseks *1. Sel juhul on laineoptika üks põhimõistetest – lainefront *2 – ja valguskiir üheselt seotud: kiir on suunatud piki lainefrondi normaali (Jn 1.1). Punktvalgusallikast väljub sfääriline laine, järelikult lähtuvad kõik kiired ühest ja samast punktist. Sellist kiirtekimpu nimetatakse homotsentriliseks. Lõpmatusest asuvast valgusallikast jõuab meieni tasalaine, mille vasteks geomeetrilises optikas on paralleelne kiirtekimp

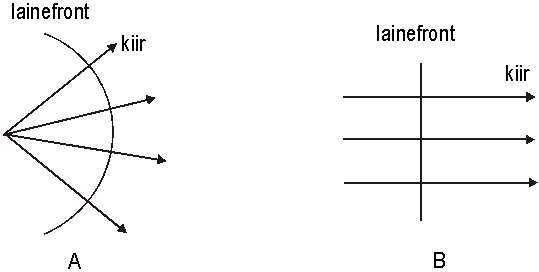
Jn 1.1 A – sfääriline laine  homotsentriline kiirtekimp; B – tasalaine  paralleelne kiirtekimp.

Valguse levikumehhanismi selgitatakse laineoptika ja geomeetrilise optika lähenduses vastavalt Huygensi ja Fermat printsiibi abil. 
Huygensi printsiibi kohaselt on lainefrondi iga punkt sfäärilise sekundaarlaine (lainekese) allikas *3. Kui on teada lainefront ajahetkel t, siis lainefrondiks ajahetkel  on esialgsest lainefrondist lähtuvate sekundaarlainete mähispind (Jn 1.2). Mingi lainekese lähtepunkti ning lainekese ja lainefrondi puutepunkti ühendav sirglõik on valguskiir so energia levikusuund.

 
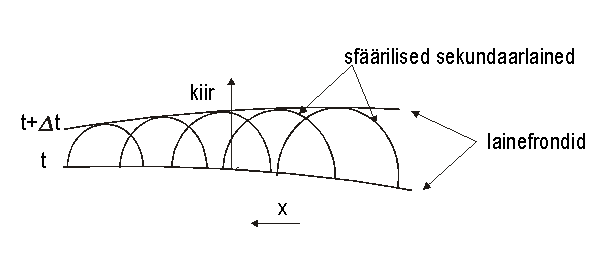
Jn 1.2 Lainefrondi leidmine vastavalt Huygensi pritsiibile; keskkond on mittehomogeenne, murdumisnäitaja n(x) kasvab paremalt vasakule.

Lainefrontide levikut peegeldumisel ja murdumisel aitab seletada ka animatsioon. 
Fermat printsiibi kohaselt levib valgus punktist A punkti B mööda teed, mille läbimiseks kulub minimaalne aeg (Jn 1.3).

 
Jn 1.3 Valguskiire levik vastavalt Fermat printsiibile; keskkond on mittehomogeenne, murdumisnäitaja n(x) kasvab paremalt vasakule.

Kiire levik peegeldumisel ja murdumisel (animatsioon)  – vaata siit.

1.2 Peegeldumis- ja murdumisseadus 
Seaduspärasused peegeldumisel olid ilmselt teada juba antiikajal, murdumisseadused leiti empiiriliselt Snell’i (Snelliuse) poolt. Peegeldumis- ja murdumisseadused võib tuletada, lähtudes nii elektromagnetlaine teooriast, Huygensi printsiibist kui ka Fermat printsiibist. 
Olgu kahe keskkonna lahutuspinnaks tasapind. Valgus, langedes lahutuspinnale (piirpinnale), osaliselt peegeldub tagasi esimesse keskkonda ja osaliselt murdub teise keskkonda. Valguse langemistasandiks nimetatakse tasandit, mis on määratud langeva kiire CO ja kiire langemispunktist O lahutuspinnale tõmmatud pinnanormaaliga (Jn 1.4).

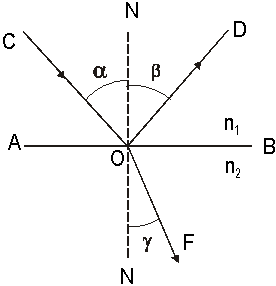
Jn 1.4 Peegeldumine ja murdumine; AB – lahutuspinna lõikejoon joonise tasandiga; CO – langev kiir; O – langemispunkt; OD – peegelduv kiir; OF – murduv kiir; NON – pinnanormaal.

Langemis-, peegeldumis- ja murdumisnurka  loetakse pinnanormaalist. 
Peegeldumis- ja murdumisseadus isotroopses keskkonnas:

• nii peegelduv kui ka murduv kiir on langemistasandis;
• peegeldumisnurk võrdub langemisnurgaga 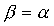 (1.1);
• antud lainepikkusel on langemis- ja murdumisnurga siinuste suhe konstantne 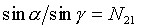 (1.2).

N₂₁ on suhteline murdumisnäitaja teise keskkonna murdumisnäitaja esimese suhtes. Kui esimeseks keskkonnaks on vaakum, siis , kus n₂ on teise keskkonna absoluutnemurdumisnäitaja *4. Murdumisnäitaja n on seotud valguse kiirusega v keskkonnas  (c – valguse kiirus vaakumis); seose (1.2) võib esitada kujul   (1.3).Kui , siis nimetatakse teist keskkonda optiliselt tihedamaks ja esimest keskkonda optiliselt hõredamaks. Optiliselt tihedamas keskkonnas on valguse levikukiirus väiksem ja mingi teepikkuse  läbimiseks kulub seal rohkem aega. Korrutist  nimetatakse optiliseks teepikkuseks.

Valguskiirt iseloomustab pööratavus: kui kiir langeb teisest keskkonnast lahutuspinnale nurga  all, siis tema murdumisnurgaks esimeses keskkonnas on .

1.3 Paralleelse kiirtekimbu murdumine

Reaalsed kiirtekimbud omavad alati lõplikku ristlõike pindala. Paralleelse kiirtekimbu puhul kujutatakse joonistel tavaliselt kiirtekimbu asemel üht kiirt (Jn 1.5A). Selline esitusviis on piisav, kui meid huvitavad vaid geomeetrilised seaduspärasused. Langeva ja murduva valguse vahelise energeetilise seose leidmisel tuleb aga arvestada, et murdumisel kiirtekimbu laius langemistasandis *5muutub (Jn 1.5B)

 (1.4).Kui , siis , murdudes optiliselt tihedamasse keskkonda kiirtekimbu laius suureneb ja energiatihedus väheneb.

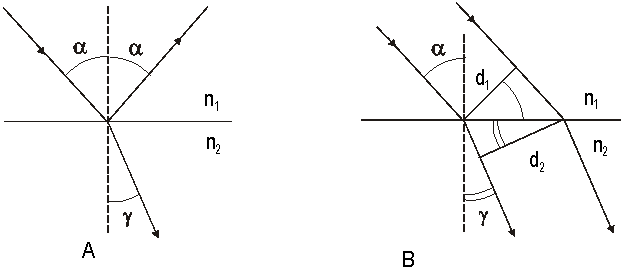
Jn 1.5 Kiir ja kiirtekimp *6

Tasaparalleelne plaat, mille paksus on  ja murdumisnäitaja n, on paljude optikaseadmete elemendiks. Jn 1.6 johtub, et plaadi läbimisel kiire siht ei muutu (kuna , siis ), toimub vaid tema paralleelnihe. Pöörates plaati ümber langemistasandiga ristuva telje O, muutub nii nihe d () kui ka optiline teepikkus Ln (L = AB). Vastavalt joonisele  ja  ning saame

optilise teepikkuse  (1.5)

ja nihke  (1.6).

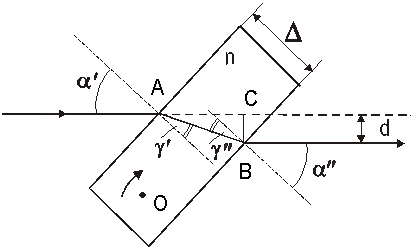
Jn 1.6 Tasaparalleelne plaat

Prismasid kasutatakse nii valguse murdmiseks kui ka peegeldamiseks. Lihtsaimal murdval prismal on kaks murdvat tahku, nende ühist serva nimetatakse prisma murdvaks servaks ning tahkudevahelist nurka prisma murdvaks nurgaks. Jn 1.7 kujutatud prisma lõiget, mis on risti prisma murdva servaga, nimetatakse prisma peatasandiks. 
Nurka   prismasse siseneva ja väljuva kiire vahel nimetatakse kaldenurgaks.

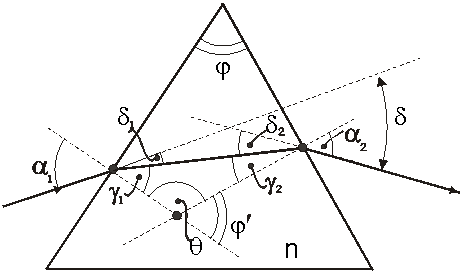
Jn 1.7 Kiire levik prismas

Leiame, kuidas muutub kaldenurk sõltuvalt langemisnurgast .

Kaldenurk  on summa kaldenurkadest  ja  prisma mõlemal murdval tahul. Jooniselt on näha, et 
 ja , seega  (1.7). 
Ristuvate haaradega nurgad on võrdsed, seega . Kuna  on  täiendnurk, saame

 (1.8).Kolmnurgast  saame  ja arvestades seost (1.8) avaldub murdev nurk      (1.9).Nüüd omandab (1.7) omandab kuju (1.10). 
Nurga  asendamiseks lähtume murdumisseadusest. Teise murdva tahu jaoks ehk *7.Vabanemaks nurgast  kasutame murdumisseadust esimese tahu jaoks . 
Kaldenurk funktsioonina langemisnurgast avaldub (1.11).Esitades sõltuvuse  graafiliselt konkreetsete ja n väärtuste jaoks ( vaata  kiire kaldenurk prismas), näeme, et eksisteerib langemisnurk, mille puhul on kiire kaldenurk minimaalne . Sel puhul öeldakse, et prisma on kaldemiinimumi asendis. 
Väidame, et prisma on kaldemiinimumi asendis, kui kiirtekäik prismas on sümmeetriline murdva nurga nurgapoolitaja suhtes, siis  ja  (Jn 1.8).

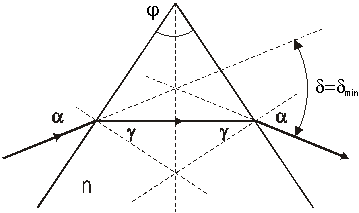
Jn 1.8 Kaldemiinimumi asend.

Oletame vastuväiteliselt, et kaldemiinimumile  vastab asümmeetriline kiirtekäik (Jn 1.7). Kui nüüd muuta kiire levikusuunda (so paremalt vasakule), siis läbib kiir sama tee, mis eelnevalt ja me saame, et kaldemiinimumile vastaks kaks erinevat langemisnurka  ja . See tulemus aga räägib vastu sõltuvusele (1.11). Seega: kaldemiinimumile vastab sümmeetriline kiirtekäik. 
Samale tulemusele jõuame ka analüütiliselt, diferentseerides avaldist (1.10) langemisnurga  järgi ja lahendades nurga  jaoks ekstreemumülesande. 
Sümmeetrilise kiirtekäigu puhul omandavad (1.7, 1.10) kuju  ja  ehk

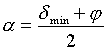     ja 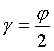 (1.12).Kasutades murdumisseadust , saame lihtsa avaldise murdumisnäitaja määramiseks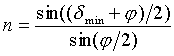   (1.13).Leidmaks mingi aine murdumisnäitajat n, valmistatakse temast prisma murdva nurgaga , leitakse prisma kaldemiinimumi asend ning määratakse nurk . Kasutades valgusallikaid, mis kiirgavad erinevatel lainepikkustel  ja arvutades valemi (1.13) järgi murdumisnäitaja, saab leida aine dispersioonikõvera . 
Olgu nüüd prisma murdev nurk väikene *8. Sel juhul võib murdumisseaduse  kirjutada kui ja (1.7) teisendub.Vastavalt avaldisele (1.9) , seega  (1.14): 
väikese murdva nurgaga prismas on kiire kaldenurk sõltumatu langemisnurgast. 
 

1.4 Optiline süsteem, kujutis

Optiline süsteem (peegel, lääts, prisma jne.) transformeerib lainefronti ehk geomeetrilise optika keeles: muudab kiirte levikusuunda. Mingi ese koosneb paljudest elementidest – eseme punktidest, millest igaüks kiirgab *9 ruumi sfäärilise laine. Kui optilisele süsteemile langev sfääriline laine transformeerub jälle sfääriliseks, on meil tegemist ideaalse optilise süsteemiga e. ideaalse süsteemi korral jääb homotsentriline kiirtekimp peale süsteemi läbimist homotsentriliseks. Optilist süsteemi läbinud kiirtekimbu tsentrit I nimetatakse punkti S kujutiseks. Ideaalse optilise süsteemi korral on punktallika S kujutis I samuti punkt, meil on tegemist stigmaatilise kujutisega. Esemeruumi punkti S ja kujutiseruumi punkti I nimetatakse kaaspunktideks. Analoogiliselt defineeritakse kaassirged, kaastasandid jne.

Kujutis võib olla tõeline (Jn 1.9) või näiv (Jn 1.10).

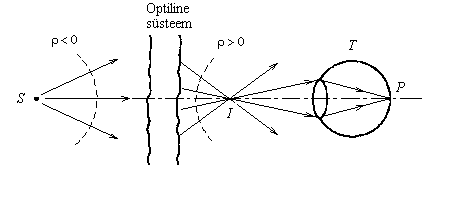
Jn 1.9 Optilise süsteemi läbimisel tekib tõeline kujutis: I-s koonduvad kiired. S – allikas; I – kujutis; – lainefrondi kõverusraadius; T– kiirguse vastuvõtja (tajur).

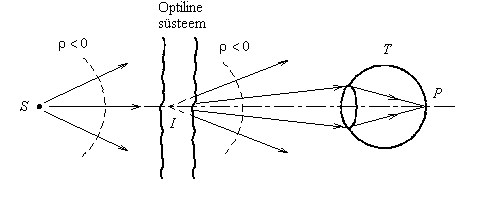
Jn 1.10 Optilise süsteemi läbimisel tekib näiv kujutis: I-s lõikuvad kiirte pikendused. Tähised vt Jn 1.9.

Sõltumata sellest, kas kujutis on tõeline või näiv, kutsub tajuri T koste (silmas – valgusaistingu, fotoaparaadis – filmi tumenemise, CCD – kaameras – laengu kogunemise jne.) esile tema valgustundliku elemendini P jõudev kiirgusvoog. Seega on näiv kujutis sama reaalne nagu tõeline kujutis. Ainus erinevus tõelisest kujutisest seisneb selles, et paigutades I asukohta (Jn 1.10) ekraani, ei teki ekraanil kujutist. 
Peegeldumine tasapinnalt. Langegu esemepunktist S tasapeeglile sfääriline laine (Jn 1.11). Mida suurem on kaugus x punktist S tõmmatud pinnanormaali ja kiire langemispunkti A vahel, seda suurem on ka peegeldumisnurk ja seetõttu kiired ei lõiku – meil on tegemist näiva kujutisega. Mistahes kaugusel x on kolmnurk SAI võrdhaarne, seega võrdub kujutise kaugus peeglist alati allika S vastava kaugusega (). Peegelduv kiirtekimp on homotsentriline ja kujutis – stigmaatiline.

 
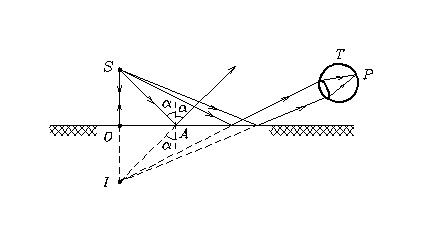
Jn 1.11 Peegeldumine tasapeeglis

Peegeldumisel vahetatakse ringi parem ja vasak pool: Jn 1.12 paikneb ese S koordinaatide alguspunktist paremal, kujutis I aga paikneb koordinaatide alguspunktist vasakul. Koordinaatteljestik  moodustab parempoolse, aga  – vasakpoolse kolmiku. Seega tranformeerub parempoolse keermega kruvi peegeldumisel vasakpoolse keermega kruviks. 
xy tasandis paikneva X – kujulise objekti peegelkujutis ei erine objektist endast; kõneldakse, et objekt omab peegelsümmeetriat. L – kujulisel objektil peegelsümmeetria puudub.

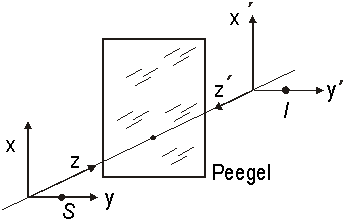
Jn 1.12 Vasak – parema vahekord peegeldumisel

Peegeldumine sfäärilisel pinnal. Langegu nõguspeeglile kõverusraadiusega  paralleelne kiirtekimp st ese paikneb lõpmatuses (Jn 1.13).

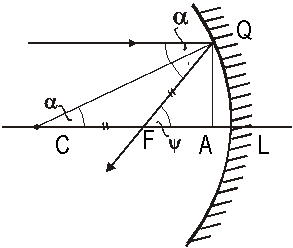
Jn 1.13 Peegeldumine sfäärilisel pinnal

Kujutis tekib peegelduva kiire ja optilise telje lõikepunktis F. Leiame kujutise asukoha sõltuvalt langeva kiire kaugusest optilisest teljest . Kuna kolmnurk CQF on võrdhaarne (), siis  ehk . Avaldame kauguse h kolmnurkadest CQA ja FQA

 ja . 
Kombineerides avaldisi saame 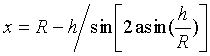 (1.15);kujutise asukoht muutub sõltuvalt sellest, kui kaugel on langev kiir optilisest teljest (vt peegeldumine sfäärilisel pinnal). Seega ei saa me enam eseme punktist stigmaatilist kujutist.

Murdumine tasapinnal. Olgu valgusallikas S optiliselt tihedamas keskkonnas (Jn 1.14), .

 
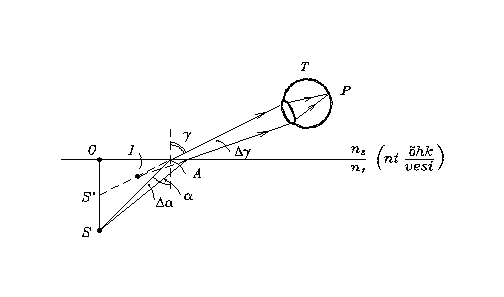
Jn 1.14. Murdumine tasapinnal

Teise keskkonda murduv kiirtekimp on hajuv, seega on kujutis näiv ja ta asetseb murduvate kiirte pikenduste lõikepunktis. Nurga  all murduva kiire pikendus lõikab pinnanormaali SO punktisS’. Kolmnurkadest SOA ja S’OA saame seose . Kuna vastavalt murdumisseadusele , siis  ja lõikepunkti S’asukoht on erinevate vaatesihtide puhul  erinev. Antud vaatesihile (mis on iseloomustatav nurgaga ) vastava kujutise I asukoht on määratud tajurini T jõudvate kiirte pikenduste lõikepunktiga. Kuna nurk  on reeglina väike, siis võib antud vaatesihis registreeritavat näivat kujutist lugeda punktiks.

Jn 1.15 on toodud erinevatele vaatesihtidele 1, 2, 3 vastavad kujutised I₁, I₂, I₃, mis paiknevad pöördpinnal, mille lõikejoon tasandiga on esitatud rasvaselt. Murdumisel tekkiv kiirtekimp ei ole enam homotsentriline, punktallikale S ei vasta enam punktkujutis ja me kõneleme astigmaatilisest kujutisest.

 
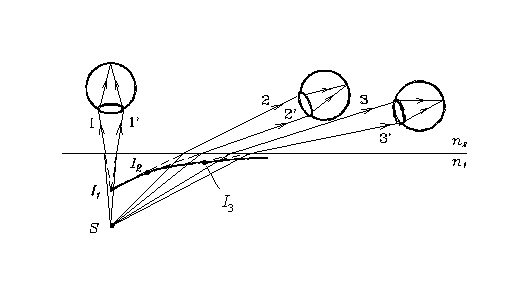
Jn 1.15 Kujutise asukoha sõltuvus vaatesihist.

Murdumine sfäärilisel pinnal.

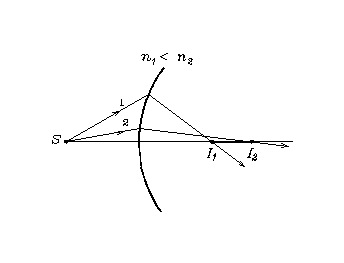Jn 1.16. Murdumine sfäärilisel pinnalKa murdumisel sfääriliselt pinnal (Jn 1.16) on tekkiv kujutis on astigmaatiline – punkti S kujutiseks on lõpliku pikkusega lõik I₁I₂.

Peegeldumise ja murdumise üldjuhul

• sfääriline laine ei jää enam sfääriliseks;
• homotsentriline kiirtekimp ei jää homotsentriliseks;
• punkti kujutis ei ole stigmaatiline.

Sisuliselt on toodud kolm järeldust ühe ja sama fakti väljendused, kuid kasutatavad mõisted on erinevad.